这是一个关于深度学习的实践教程。我们将逐步构建一个解决方案，用于面部关键点检测 Kaggle 挑战。该教程介绍了Lasagne，这是一个用于使用 Python 和Theano构建神经网络的新库。我们将使用 Lasagne 实现一些网络架构，讨论数据增强、dropout、动量的重要性以及预训练。其中一些方法将帮助我们大幅改善结果。

我假设你已经对神经网络有相当多的了解。这是因为我们不会讨论神经网络工作背后的许多背景知识；有一些很好的书籍和视频可以提供这方面的信息，比如《神经网络与深度学习》在线书籍。Alec Radford的演讲使用Python的Theano库进行深度学习是一个很好的快速介绍。确保你也查看Andrej Karpathy令人惊叹的ConvNetJS浏览器演示。

如果您只想跟着操作，无需自己输入代码并执行。但以下是供那些拥有CUDA兼容GPU并希望自行运行实验的人的安装说明。

我假设您已安装了CUDA工具包、Python 2.7.x、numpy、pandas、matplotlib和scikit-learn。要安装其余的依赖项，如Lasagne和Theano，请运行以下命令：

pip install -r https://raw.githubusercontent.com/dnouri/kfkd-tutorial/master/requirements.txt

(请注意，出于简洁起见，我没有包括创建 virtualenv 并激活它的命令。但你应该这样做。)

如果一切正常，您应该能够在您的虚拟环境中找到 src/lasagne/examples/ 目录，并运行MNIST示例。这是神经网络的"Hello, world"。有十个类别，每个类别代表0到9之间的一个数字，输入是尺寸为28x28的手写数字的灰度图像。

cd src/lasagne/examples/ python mnist.py

这个命令将在大约三十秒后开始打印输出。它需要一段时间的原因是Lasagne使用Theano来进行繁重的工作；而Theano本身是一个“在Python中优化GPU元编程代码生成数组导向优化数学编译器”，它将生成需要编译的C代码，然后才能进行训练。幸运的是，我们只需要在第一次运行时为这种开销付出代价。

一旦培训开始，您将看到如下输出：

第1个时期的500 训练损失: 1.352731 验证损失: 0.466565 验证准确率: 87.70 % 第2个时期的500 训练损失: 0.591704 验证损失: 0.326680 验证准确率: 90.64 % 第3个时期的500 训练损失: 0.464022 验证损失: 0.275699 验证准确率: 91.98 % ...

如果你让训练运行足够长的时间，你会注意到大约在75个epochs之后，测试准确率会达到约98%。

如果您有GPU，您会想要配置Theano来使用它。您需要在主目录中创建一个名为~/.theanorc的文件，内容类似于以下内容：

[全局] floatX = float32 device = gpu0 [库] cnmem = 1

(如果本教程中的任何指令对您无效，请在此处提交错误报告。)

Facial Keypoint Detection挑战的训练数据集包含7,049张96x96的灰度图像。对于每张图像，我们应该学会找到15个关键点的正确位置（x和y坐标），例如left_eye_center、right_eye_outer_corner、mouth_center_bottom_lip等。

一个示例，其中一个脸部有三个关键点标记。

数据集中有一个有趣的变化是，对于一些关键点，我们只有约2,000个标签，而其他关键点则有超过7,000个标签可用于训练。

让我们编写一些 Python 代码，从提供的 CSV 文件中加载数据。我们将编写一个可以加载训练数据和测试数据的函数。这两个数据集的不同之处在于测试数据不包含目标值；挑战的目标是预测这些值。这是我们的 load() 函数：

# 文件 kfkd.py
import os import numpy as np
from pandas.io.parsers import read_csv
from sklearn.utils import shuffle FTRAIN = '~/data/kaggle-facial-keypoint-detection/training.csv'
FTEST = '~/data/kaggle-facial-keypoint-detection/test.csv' def load(test=False, cols=None): """Loads data from FTEST if *test* is True, otherwise from FTRAIN.
 Pass a list of *cols* if you're only interested in a subset of the
 target columns.
 """ fname = FTEST if test else FTRAIN df = read_csv(os.path.expanduser(fname)) # load pandas dataframe # The Image column has pixel values separated by space; convert # the values to numpy arrays: df['Image'] = df['Image'].apply(lambda im: np.fromstring(im, sep=' ')) if cols: # get a subset of columns df = df[list(cols) + ['Image']] print(df.count()) # prints the number of values for each column df = df.dropna() # drop all rows that have missing values in them X = np.vstack(df['Image'].values) / 255. # scale pixel values to [0, 1] X = X.astype(np.float32) if not test: # only FTRAIN has any target columns y = df[df.columns[:-1]].values y = (y - 48) / 48 # scale target coordinates to [-1, 1] X, y = shuffle(X, y, random_state=42) # shuffle train data y = y.astype(np.float32) else: y = None return X, y X, y = load()
print("X.shape == {}; X.min == {:.3f}; X.max == {:.3f}".format( X.shape, X.min(), X.max()))
print("y.shape == {}; y.min == {:.3f}; y.max == {:.3f}".format( y.shape, y.min(), y.max()))

你不必浏览此函数的每一个细节。但让我们看看上面的脚本输出的内容：

$ python kfkd.py left_eye_center_x 7034 left_eye_center_y 7034 right_eye_center_x 7032 right_eye_center_y 7032 left_eye_inner_corner_x 2266 left_eye_inner_corner_y 2266 left_eye_outer_corner_x 2263 left_eye_outer_corner_y 2263 right_eye_inner_corner_x 2264 right_eye_inner_corner_y 2264 ... mouth_right_corner_x 2267 mouth_right_corner_y 2267 mouth_center_top_lip_x 2272 mouth_center_top_lip_y 2272 mouth_center_bottom_lip_x 7014 mouth_center_bottom_lip_y 7014 Image 7044 dtype: int64 X.shape == (2140, 9216); X.min == 0.000; X.max == 1.000 y.shape == (2140, 30); y.min == -0.920; y.max == 0.996

首先，它会打印出CSV文件中所有列的列表，以及每列可用值的数量。因此，虽然在训练数据的所有行中都有图像，但对于mouth_right_corner_x等列，我们只有2,267个值。

load() 返回一个元组 (X, y)，其中 y 是目标矩阵。 y 的形状为 n x m，其中 n 是数据集中具有所有 m 个关键点的样本数。删除所有具有缺失值的行是这行代码的作用：

删除所有包含缺失值的行

脚本的输出 y.shape == (2140, 30) 告诉我们数据集中只有 2,140 张图像同时具有所有 30 个目标数值。最初，我们将仅使用这 2,140 个样本进行训练。这导致输入维度（9,216）比样本数量多得多；这表明过拟合可能会成为一个问题。让我们看看。当然，随意丢弃 70% 的训练数据是一个坏主意，我们稍后会讨论这个问题。

load()函数的另一个特性是将图像像素的强度值缩放到区间[0, 1]，而不是0到255。目标值（x和y坐标）被缩放到[-1, 1]；之前它们的取值范围是0到95。

net1对象实际上会记录在表中打印出的数据。我们可以通过train_history_属性访问该记录。让我们绘制这两条曲线：

train_loss = np.array([i["train_loss"] for i in net1.train_history_]) valid_loss = np.array([i["valid_loss"] for i in net1.train_history_]) pyplot.plot(train_loss, linewidth=3, label="train") pyplot.plot(valid_loss, linewidth=3, label="valid") pyplot.grid() pyplot.legend() pyplot.xlabel("epoch") pyplot.ylabel("loss") pyplot.ylim(1e-3, 1e-2) pyplot.yscale("log") pyplot.show()

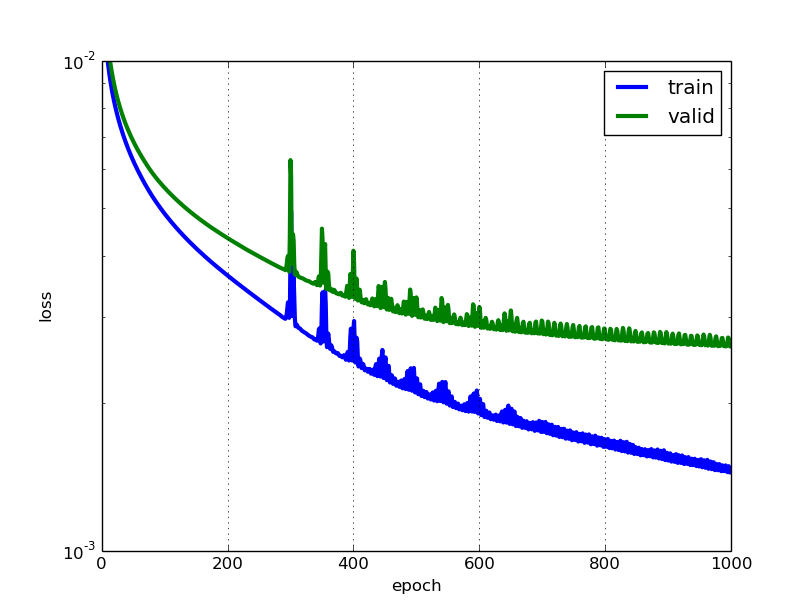
我们可以看到我们的网络出现了过拟合，但情况并不那么糟糕。特别是，我们没有看到验证错误再次变得更糟的点，因此看起来 提前停止 这种通常用于避免过拟合的技术在这一点上并不会很有用。请注意，除了选择隐藏层中少量神经元之外，我们根本没有使用任何正则化，这种设置将在一定程度上控制过拟合。

那么，网络的预测是什么样子的呢？让我们从测试集中挑选几个例子来检查：

def plot_sample(x, y, axis): img = x.reshape(96, 96) axis.imshow(img, cmap='gray') axis.scatter(y[0::2] * 48 + 48, y[1::2] * 48 + 48, marker='x', s=10) X, _ = load(test=True) y_pred = net1.predict(X) fig = pyplot.figure(figsize=(6, 6)) fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05) for i in range(16): ax = fig.add_subplot(4, 4, i + 1, xticks=[], yticks=[]) plot_sample(X[i], y_pred[i], ax) pyplot.show()

我们第一个模型对从测试集中取出的16个样本的预测。

预测看起来合理，但有时候相差还是挺大的。让我们试着做得更好一点。

LeNet5风格的卷积神经网络是深度学习在计算机视觉领域取得突破的核心。卷积层与全连接层不同；它们使用一些技巧来减少需要学习的参数数量，同时保持高表达能力。这些技巧包括：

• 局部连接性: 神经元仅连接到前一层的部分神经元，
• 权重共享: 卷积层中的一部分神经元之间共享权重（这些神经元形成所谓的 特征图），
• 池化: 输入的静态子采样。

卷积层中的单元实际上连接到前一层中的一个二维神经元块，这使它们能够利用输入中的二维结构。

在Lasagne中使用卷积层时，我们必须准备输入数据，使得每个样本不再是一个由9216个像素强度组成的平面向量，而是一个形状为_(c, 0, 1)的三维矩阵，其中c是通道数（颜色数），0和1对应于输入图像的x和y维度。在我们的情况下，具体的形状将是(1, 96, 96)_，因为我们只处理单个（灰度）颜色通道。

一个函数 load2d，它包装了先前编写的 load 函数并进行必要的转换，很容易编码：

def load2d(test=False, cols=None): X, y = load(test=test) X = X.reshape(-1, 1, 96, 96) return X, y

我们将构建一个具有三个卷积层和两个全连接层的卷积神经网络。每个卷积层后面都跟着一个2x2的最大池化层。从32个滤波器开始，我们每个卷积层都会将滤波器数量翻倍。密集连接的隐藏层都有500个单元。

再次，没有采用权重衰减或丢弃法进行正则化。事实证明，使用非常小的卷积滤波器，比如我们的3x3和2x2滤波器，本身就是一个相当不错的正则化方法。

让我们写下代码：

net2
= NeuralNet( layers=[ ('input', layers.InputLayer), ('conv1', layers.Conv2DLayer), ('pool1', layers.MaxPool2DLayer), ('conv2', layers.Conv2DLayer), ('pool2', layers.MaxPool2DLayer), ('conv3', layers.Conv2DLayer), ('pool3', layers.MaxPool2DLayer), ('hidden4', layers.DenseLayer), ('hidden5', layers.DenseLayer), ('output', layers.DenseLayer), ], input_shape=(None, 1, 96, 96), conv1_num_filters=32, conv1_filter_size=(3, 3), pool1_pool_size=(2, 2), conv2_num_filters=64, conv2_filter_size=(2, 2), pool2_pool_size=(2, 2), conv3_num_filters=128, conv3_filter_size=(2, 2), pool3_pool_size=(2, 2), hidden4_num_units=500, hidden5_num_units=500, output_num_units=30, output_nonlinearity=None, update_learning_rate=0.01, update_momentum=0.9, regression=True, max_epochs=1000, verbose=1, ) X, y = load2d() # load 2-d data net2.fit(X, y) # Training for 1000 epochs will take a while. We'll pickle the

trained model so that we can load it back later:

import cPickle as pickle with open('net2.pickle', 'wb') as f: pickle.dump(net2, f, -1)

训练这个神经网络的计算成本比我们训练的第一个要高得多。训练时间大约是第一个的15倍；即使在一台强大的GPU上，这1000个时代也需要超过20分钟。

然而，我们的耐心得到了回报，现在的模型比之前的要好得多。让我们来看看运行脚本时的输出。首先是带有其输出形状的层列表。请注意，第一个卷积层产生了大小为_(94, 94)_的32个输出图像，即每个滤波器产生一个94x94的输出图像：

InputLayer (None, 1, 96, 96) 产生 9216 输出 Conv2DCCLayer (None, 32, 94, 94) 产生 282752 输出 MaxPool2DCCLayer (None, 32, 47, 47) 产生 70688 输出 Conv2DCCLayer (None, 64, 46, 46) 产生 135424 输出 MaxPool2DCCLayer (None, 64, 23, 23) 产生 33856 输出 Conv2DCCLayer (None, 128, 22, 22) 产生 61952 输出 MaxPool2DCCLayer (None, 128, 11, 11) 产生 15488 输出 DenseLayer (None, 500) 产生 500 输出 DenseLayer (None, 500) 产生 500 输出 DenseLayer (None, 30) 产生 30 输出

接下来是与第一个示例中相同的表，显示随时间变化的训练和验证错误：

Epoch | 训练损失 | 验证损失 | 训练 / 验证 --------|--------------|--------------|---------------- 1 | 0.111763 | 0.042740 | 2.614934 2 | 0.018500 | 0.009413 | 1.965295 3 | 0.008598 | 0.007918 | 1.085823 4 | 0.007292 | 0.007284 | 1.001139 5 | 0.006783 | 0.006841 | 0.991525 ... 500 | 0.001791 | 0.002013 | 0.889810 501 | 0.001789 | 0.002011 | 0.889433 502 | 0.001786 | 0.002009 | 0.889044 503 | 0.001783 | 0.002007 | 0.888534 504 | 0.001780 | 0.002004 | 0.888095 505 | 0.001777 | 0.002002 | 0.887699 ... 995 | 0.001083 | 0.001568 | 0.690497 996 | 0.001082 | 0.001567 | 0.690216 997 | 0.001081 | 0.001567 | 0.689867 998 | 0.001080 | 0.001567 | 0.689595 999 | 0.001080 | 0.001567 | 0.689089 1000 | 0.001079 | 0.001566 | 0.688874

第一个网络相比有了很大的改进。我们的 RMSE 看起来也相当不错：

">>> np.sqrt(0.001566) * 48 1.8994904579913006

我们可以使用测试集中更有问题的样本之一来比较这两个网络的预测：

sample1
= load(test=True)[0][6:7] sample2
= load2d(test=True)[0][6:7] y_pred1
= net1.predict(sample1)[0] y_pred2
= net2.predict(sample2)[0] fig
= pyplot.figure(figsize=(6, 3)) ax
= fig.add_subplot(1, 2, 1, xticks=[], yticks=[]) plot_sample(sample1[0], y_pred1, ax) ax
= fig.add_subplot(1, 2, 2, xticks=[], yticks=[]) plot_sample(sample1[0], y_pred2, ax) pyplot.show()

左侧 net1 的预测与 net2 的预测进行比较。

然后让我们比较第一个和第二个网络的学习曲线：

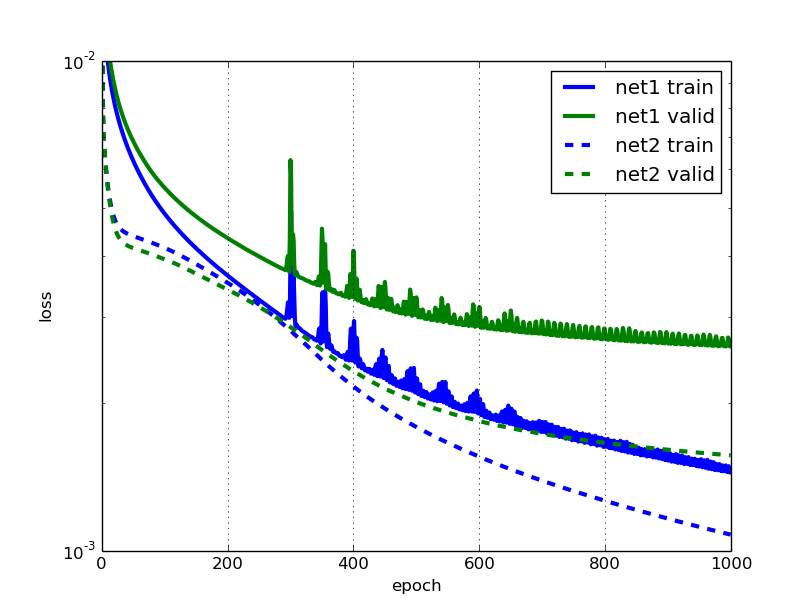
这看起来相当不错，我喜欢新错误曲线的平滑度。但我们注意到，在接近结尾时，net2的验证错误比训练错误更快地趋于平缓。我敢打赌，通过使用更多的训练样本，我们可以改进这一点。如果我们水平翻转输入图像会怎样；这样做能否通过增加训练数据量来改善训练效果？

通过使用更多的训练数据，通常可以使过拟合的神经网络表现更好。（如果您的未经正则化的神经网络没有过拟合，那么您可能应该将其扩大。）

数据增强让我们通过应用转换、添加噪声等方式，人为地增加训练样本的数量。这显然比不得不亲自外出收集更多样本更经济。增强是深度学习工具箱中非常有用的工具。

我们已经简要提到了批处理迭代器。批处理迭代器的工作是将样本矩阵分成批次，我们的情况下每批次大小为128。在分批的同时，批处理迭代器还可以实时对数据应用变换。因此，为了生成那些水平翻转，我们实际上不必在输入矩阵中增加训练数据的数量。相反，我们只需在迭代数据时以50%的概率执行水平翻转。这很方便，对于某些问题，它使我们能够生成无限数量的示例，而不会增加内存使用量。此外，对输入图像的变换可以在GPU忙于处理上一批次时完成，因此几乎没有额外成本。

水平翻转图像只是使用切片的问题：

X, y
= load2d() X_flipped = X[:, :, :, ::-1] \

simple slice to flip all images \

plot two images:

fig = pyplot.figure(figsize=(6, 3)) ax = fig.add_subplot(1, 2, 1, xticks=[], yticks=[]) plot_sample(X[1], y[1], ax) ax = fig.add_subplot(1, 2, 2, xticks=[], yticks=[]) plot_sample(X_flipped[1], y[1], ax) pyplot.show()

左侧显示原始图像，右侧是翻转后的图像。

在右侧的图片中，请注意目标值关键点不再与图像对齐。由于我们翻转了图像，我们必须确保也翻转目标值。为了做到这一点，我们不仅需要翻转坐标，还需要交换目标值的位置；这是因为翻转后的左眼中心点坐标不再指向翻转后图像中的左眼；现在它对应右眼中心点坐标。一些点，比如鼻尖的y坐标不受影响。我们将定义一个元组flip_indices，其中包含了在水平翻转图像时需要交换位置的目标向量中的哪些列的信息。请记住，列的列表如下：

left_eye_center_x 7034 left_eye_center_y 7034 right_eye_center_x 7032 right_eye_center_y 7032 left_eye_inner_corner_x 2266 left_eye_inner_corner_y 2266 ...

由于 left_eye_center_x 需要与 right_eye_center_x 交换位置，我们写下元组 (0, 2)。同样，left_eye_center_y 需要与 right_eye_center_y 交换位置。因此我们写下 (1, 3)，依此类推。最终，我们得到：

flip_indices = [(0, 2), (1, 3), (4, 8), (5, 9), (6, 10), (7, 11), (12, 16), (13, 17), (14, 18), (15, 19), (22, 24), (23, 25)] # 让我们看看是否正确： df = read_csv(os.path.expanduser(FTRAIN)) for i, j in flip_indices: print("# {} -> {}".format(df.columns[i], df.columns[j])) # 这将打印出： # left_eye_center_x -> right_eye_center_x # left_eye_center_y -> right_eye_center_y # left_eye_inner_corner_x -> right_eye_inner_corner_x # left_eye_inner_corner_y -> right_eye_inner_corner_y # left_eye_outer_corner_x -> right_eye_outer_corner_x # left_eye_outer_corner_y -> right_eye_outer_corner_y # left_eyebrow_inner_end_x -> right_eyebrow_inner_end_x # left_eyebrow_inner_end_y -> right_eyebrow_inner_end_y # left_eyebrow_outer_end_x -> right_eyebrow_outer_end_x # left_eyebrow_outer_end_y -> right_eyebrow_outer_end_y # mouth_left_corner_x -> mouth_right_corner_x # mouth_left_corner_y -> mouth_right_corner_y

我们的批处理迭代器实现将从默认的BatchIterator类派生，并仅覆盖transform()方法。让我们看看当我们把它们放在一起时是什么样子：

from nolearn.lasagne import BatchIterator class FlipBatchIterator(BatchIterator): flip_indices = [(0, 2), (1, 3), (4, 8), (5, 9), (6, 10), (7, 11), (12, 16), (13, 17), (14, 18), (15, 19), (22, 24), (23, 25), ] def transform(self, Xb, yb): Xb, yb = super(FlipBatchIterator, self).transform(Xb, yb) # Flip half of the images in this batch at random: bs = Xb.shape[0] indices = np.random.choice(bs, bs / 2, replace=False) Xb[indices] = Xb[indices, :, :, ::-1] if yb is not None: # Horizontal flip of all x coordinates: yb[indices, ::2] = yb[indices, ::2] * -1 # Swap places, e.g. left_eye_center_x -> right_eye_center_x for a, b in self.flip_indices: yb[indices, a], yb[indices, b] = ( yb[indices, b], yb[indices, a]) return Xb, yb

要使用这个批处理迭代器进行训练，我们将把它作为 batch_iterator_train 参数传递给 NeuralNet。让我们定义 net3，一个网络，它看起来与 net2 完全相同，只是在最后几行有所不同：

net3
= NeuralNet(

regression=True, batch_iterator_train=FlipBatchIterator(batch_size=128), max_epochs=3000, verbose=1, )

现在我们正在传递我们的FlipBatchIterator，但我们也将训练的时代数量增加了三倍。虽然我们每一个训练时代仍然会查看与之前相同数量的示例（毕竟，我们没有改变X的大小），但事实证明，当我们使用我们的转换FlipBatchIterator时，训练时间会变得更长。这是因为网络学到的东西这次更具一般性，而学习具有一般性的东西可能比过拟合更难。

所以这可能需要一个小时来训练。让我们确保在训练结束时将模型保存起来，然后我们就可以去拿一些茶和饼干。或者也许去洗衣服：

net3.fit(X, y) import cPickle as pickle with open('net3.pickle', 'wb') as f: pickle.dump(net3, f, -1)

$ python kfkd.py ... Epoch | 训练损失 | 验证损失 | 训练 / 验证 --------|--------------|--------------|---------------- ... 500 | 0.002238 | 0.002303 | 0.971519 ... 1000 | 0.001365 | 0.001623 | 0.841110 1500 | 0.001067 | 0.001457 | 0.732018 2000 | 0.000895 | 0.001369 | 0.653721 2500 | 0.000761 | 0.001320 | 0.576831 3000 | 0.000678 | 0.001288 | 0.526410

与net2的学习相比，我们注意到在3000个时期后，数据增强的网络在验证集上的错误确实要小约5%。我们可以看到net2在2000个时期左右停止学习任何有用的东西，变得非常嘈杂，而net3则继续改善其验证错误，尽管进展缓慢。

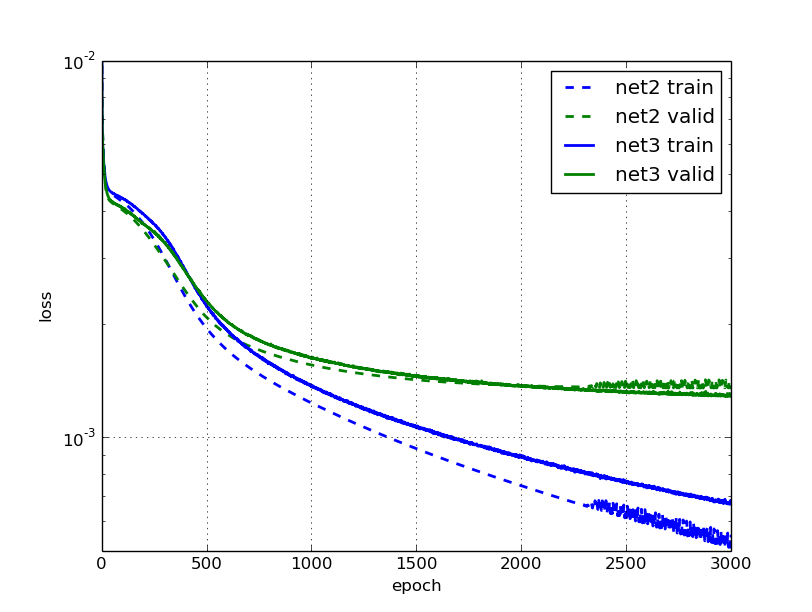
看起来为了微小的收益而付出了很多努力？我们将在下一部分找出是否值得。

我们上一个模型令人讨厌的地方在于，训练它已经花了一个小时，不用等待实验结果这么长时间确实让人没有动力。在本节中，我们将讨论两种技巧的组合，以解决这个问题，让神经网络再次训练得更快。

开始时使用较高的学习率并在训练过程中逐渐降低的直觉是：当我们开始训练时，我们离最优解还很远，我们希望迈大步向最优解靠近并快速学习。但是当我们接近最优解时，我们希望迈小步。这就像乘火车回家，但当你进门时，你是步行而不是坐火车。

在深度学习中初始化和动量的重要性是一次由Ilya Sutskever等人发表的演讲和论文的标题。在这里，我们了解到另一个提升深度学习效果的有用技巧：即在训练过程中增加优化方法的动量参数。原文链接

记住，在我们之前的模型中，我们分别使用静态的0.01和0.9来初始化学习率和动量。让我们改变这一点，使得学习率随着时代的增加而线性减少，同时让动量增加。

NeuralNet 允许我们使用 on_epoch_finished 钩子在训练过程中更新参数。我们可以将一个函数传递给 on_epoch_finished，每当一个 epoch 完成时就会调用它。然而，在我们可以动态地为 update_learning_rate 和 update_momentum 分配新值之前，我们必须将这两个参数更改为 Theano 共享变量。幸运的是，这相当容易：

import theano def float32(k): return np.cast'float32' net4 = NeuralNet( # ... update_learning_rate=theano.shared(float32(0.03)), update_momentum=theano.shared(float32(0.9)), # ... )

我们传递的回调函数或回调函数列表将使用两个参数调用：nn，即神经网络实例本身，以及train_history，它与nn.train_history_相同。

而不是使用硬编码值的回调函数，我们将使用一个具有 \call\ 方法的可参数化类作为我们的回调。让我们称这个类为 AdjustVariable。实现相当直接：

class AdjustVariable(object): def \_init\_(self, name, start=0.03, stop=0.001): self.name = name self.start, self.stop = start, stop self.ls = None def \_call\_(self, nn, train_history): if self.ls is None: self.ls = np.linspace(self.start, self.stop, nn.max_epochs) epoch = train_history[-1]['epoch'] new_value = float32(self.ls[epoch - 1]) getattr(nn, self.name).set_value(new_value)

现在让我们把所有东西都插在一起，然后我们就准备好开始训练了：

net4
= NeuralNet( \

... update_learning_rate=theano.shared(float32(0.03)), update_momentum=theano.shared(float32(0.9)), \

... regression=True, \

batch_iterator_train=FlipBatchIterator(batch_size=128), on_epoch_finished=[ AdjustVariable('update_learning_rate', start=0.03, stop=0.0001), AdjustVariable('update_momentum', start=0.9, stop=0.999), ], max_epochs=3000, verbose=1, ) X, y = load2d() net4.fit(X, y) with open('net4.pickle', 'wb') as f: pickle.dump(net4, f, -1)

我们将训练两个网络：net4不使用我们的FlipBatchIterator，net5使用。除此之外，它们是相同的。

这是 net4 的学习：

Epoch | 训练损失 | 验证损失 | 训练 / 验证 --------|--------------|--------------|---------------- 50 | 0.004216 | 0.003996 | 1.055011 100 | 0.003533 | 0.003382 | 1.044791 250 | 0.001557 | 0.001781 | 0.874249 500 | 0.000915 | 0.001433 | 0.638702 750 | 0.000653 | 0.001355 | 0.481806 1000 | 0.000496 | 0.001387 | 0.357917

Cool, 训练现在进行得快多了！在500和1000个时代时的训练误差是net2之前的一半，这是在我们调整学习率和动量之前。这次，泛化似乎在大约750个时代后就停止改进了；看起来训练时间再长也没有意义。

打开数据增强功能的 net5 怎么样？

Epoch | 训练损失 | 验证损失 | 训练 / 验证 --------|--------------|--------------|---------------- 50 | 0.004317 | 0.004081 | 1.057609 100 | 0.003756 | 0.003535 | 1.062619 250 | 0.001765 | 0.001845 | 0.956560 500 | 0.001135 | 0.001437 | 0.790225 750 | 0.000878 | 0.001313 | 0.668903 1000 | 0.000705 | 0.001260 | 0.559591 1500 | 0.000492 | 0.001199 | 0.410526 2000 | 0.000373 | 0.001184 | 0.315353

再次，我们的训练速度比net3快得多，并且结果更好。1000个epochs后，我们的效果比net3在3000个epochs后更好。而且，使用数据增强训练的模型现在在验证错误方面比没有使用数据增强的模型好约10%。

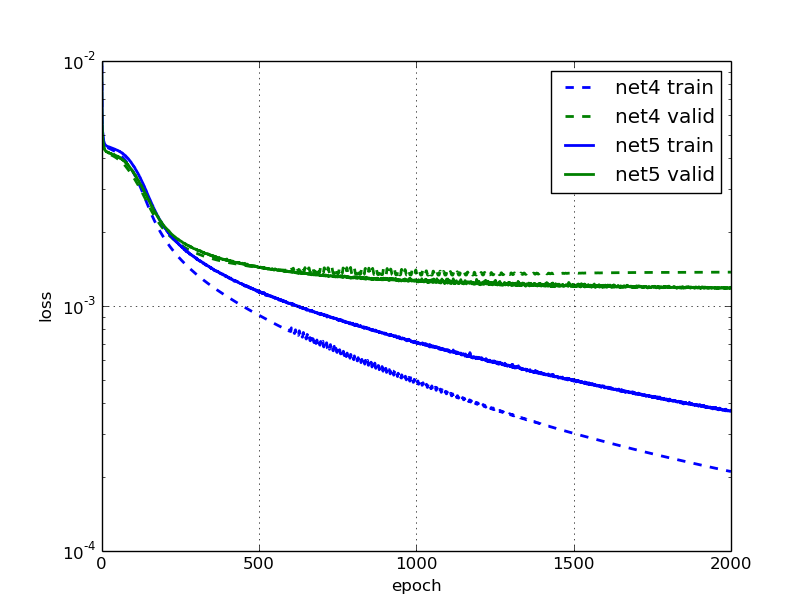
2012年在通过防止特征检测器共适应来改进神经网络论文中引入的dropout是一种非常有效的流行正则化技术。我不会详细解释为什么它如此有效，你可以在其他地方阅读相关内容。

与任何其他正则化技术一样，dropout 只有在我们有一个过拟合的网络时才有意义，这显然是我们在前一节训练的 net5 网络的情况。重要的是要记住先让你的网络训练得很好并过拟合，然后再进行正则化。

要在Lasagne中使用dropout，我们将在现有层之间添加DropoutLayer层，并为每个层分配dropout概率。这是我们新网络的完整定义。我在这些行和net5之间添加的行末尾添加了一个# !注释。

net6 = NeuralNet( layers=[ ('input', layers.InputLayer), ('conv1', layers.Conv2DLayer), ('pool1', layers.MaxPool2DLayer), ('dropout1', layers.DropoutLayer), # ! ('conv2', layers.Conv2DLayer), ('pool2', layers.MaxPool2DLayer), ('dropout2', layers.DropoutLayer), # ! ('conv3', layers.Conv2DLayer), ('pool3', layers.MaxPool2DLayer), ('dropout3', layers.DropoutLayer), # ! ('hidden4', layers.DenseLayer), ('dropout4', layers.DropoutLayer), # ! ('hidden5', layers.DenseLayer), ('output', layers.DenseLayer), ], input_shape=(None, 1, 96, 96), conv1_num_filters=32, conv1_filter_size=(3, 3), pool1_pool_size=(2, 2), dropout1_p=0.1, # ! conv2_num_filters=64, conv2_filter_size=(2, 2), pool2_pool_size=(2, 2), dropout2_p=0.2, # ! conv3_num_filters=128, conv3_filter_size=(2, 2), pool3_pool_size=(2, 2), dropout3_p=0.3, # ! hidden4_num_units=500, dropout4_p=0.5, # ! hidden5_num_units=500, output_num_units=30, output_nonlinearity=None, update_learning_rate=theano.shared(float32(0.03)), update_momentum=theano.shared(float32(0.9)), regression=True, batch_iterator_train=FlipBatchIterator(batch_size=128), on_epoch_finished=[ AdjustVariable('update_learning_rate', start=0.03, stop=0.0001), AdjustVariable('update_momentum', start=0.9, stop=0.999), ], max_epochs=3000, verbose=1, )

我们的网络现在已经足够大，可以使Python的pickle崩溃，并出现最大递归错误。因此，在保存之前，我们必须增加Python的递归限制：

import sys sys.setrecursionlimit(10000) X, y
= load2d() net6.fit(X, y) import cPickle as pickle with open('net6.pickle', 'wb') as f: pickle.dump(net6, f, -1)

观察学习过程，我们注意到它又变慢了，这在使用了辍学时是可以预料的，但最终它将胜过 net5:

| 时期 | 训练损失 | 验证损失 | 训练 / 验证 --------|--------------|--------------|--------------- 50 | 0.004619 | 0.005198 | 0.888566 100 | 0.004369 | 0.004182 | 1.044874 250 | 0.003821 | 0.003577 | 1.068229 500 | 0.002598 | 0.002236 | 1.161854 1000 | 0.001902 | 0.001607 | 1.183391 1500 | 0.001660 | 0.001383 | 1.200238 2000 | 0.001496 | 0.001262 | 1.185684 2500 | 0.001383 | 0.001181 | 1.171006 3000 | 0.001306 | 0.001121 | 1.164100

过拟合现象似乎并不那么严重。不过我们需要小心那些数字：由于训练误差是使用了 dropout 进行评估，而验证误差则是在没有 dropout 的情况下评估的，所以训练和验证之间的比率现在具有稍微不同的含义。对于训练误差的一个更具可比性的值是这个：

从sklearn.metrics导入mean_squared_error print mean_squared_error(net6.predict(X), y)

输出类似于0.0010073791

在我们之前没有使用辍学的模型中，训练集上的误差为0.000373。因此，我们的辍学网络不仅表现略好，而且过拟合比之前少得多。这是个好消息，因为这意味着当我们使网络更大（更具表现力）时，我们可以期待更好的性能。接下来我们将尝试增加最后两个隐藏层中的单元数，从500增加到1000。请更新这些行：

net7
= NeuralNet(
\

... hidden4_num_units=1000, \

! dropout4_p=0.5, hidden5_num_units=1000, \

! \

... )

非丢弃层的改进现在变得更加实质性：

Epoch | 训练损失 | 验证损失 | 训练 / 验证 --------|--------------|--------------|--------------- 50 | 0.004756 | 0.007043 | 0.675330 100 | 0.004440 | 0.005321 | 0.834432 250 | 0.003974 | 0.003928 | 1.011598 500 | 0.002574 | 0.002347 | 1.096366 1000 | 0.001861 | 0.001613 | 1.153796 1500 | 0.001558 | 0.001372 | 1.135849 2000 | 0.001409 | 0.001230 | 1.144821 2500 | 0.001295 | 0.001146 | 1.130188 3000 | 0.001195 | 0.001087 | 1.099271

我们在过拟合方面仍然表现得非常出色！我觉得如果我们增加训练的轮数，这个模型可能会变得更好。让我们试一试：

net12 \( \( ... max_epochs=10000, \( ... )

| 时期 | 训练损失 | 验证损失 | 训练 / 验证 |--------|--------------|--------------|--------------- | 50 | 0.004756 | 0.007027 | 0.676810 | 100 | 0.004439 | 0.005321 | 0.834323 | 500 | 0.002576 | 0.002346 | 1.097795 | 1000 | 0.001863 | 0.001614 | 1.154038 | 2000 | 0.001406 | 0.001233 | 1.140188 | 3000 | 0.001184 | 0.001074 | 1.102168 | 4000 | 0.001068 | 0.000983 | 1.086193 | 5000 | 0.000981 | 0.000920 | 1.066288 | 6000 | 0.000904 | 0.000884 | 1.021837 | 7000 | 0.000851 | 0.000849 | 1.002314 | 8000 | 0.000810 | 0.000821 | 0.985769 | 9000 | 0.000769 | 0.000803 | 0.957842 | 10000 | 0.000760 | 0.000787 | 0.966583

所以你正在见证辍学的魔力。:-)

让我们比较一下迄今为止训练的网络及其相应的训练和验证错误：

名称 | 描述 | 轮数 | 训练损失 | 验证损失 -------|------------------|----------|--------------|-------------- net1 | 单隐藏层 | 400 | 0.002244 | 0.003255 net2 | 卷积层 | 1000 | 0.001079 | 0.001566 net3 | 数据增强 | 3000 | 0.000678 | 0.001288 net4 | 动量 + 学习率调整 | 1000 | 0.000496 | 0.001387 net5 | net4 + 增强 | 2000 | 0.000373 | 0.001184 net6 | net5 + 丢弃层 | 3000 | 0.001306 | 0.001121 net7 | net6 + 轮数 | 10000 | 0.000760 | 0.000787

记得一开始我们丢弃的那70%的训练数据吗？结果证明，如果我们想在Kaggle排行榜上获得竞争力的分数，那是一个非常糟糕的主意。那70%的数据和挑战的测试集中存在相当大的变化，而我们的模型尚未见过。

所以，我们不是训练单个模型，而是训练几个专家，每个专家预测不同的目标值集。我们将训练一个仅预测左眼中心和右眼中心的模型，一个仅预测鼻尖的模型，依此类推；总共将有六个模型。这将使我们能够使用完整的训练数据集，并希望在整体上获得更有竞争力的分数。

这六位专家都将使用完全相同的网络架构（一种简单的方法，不一定是最好的）。由于训练时间比以前要长得多，让我们考虑一种策略，这样我们就不必等待 max_epochs 完成，即使验证错误在更早的时候就停止改进。这被称为 early stopping，我们将编写另一个 on_epoch_finished 回调来处理这个问题。这是实现方式：

class EarlyStopping(object): def __init__(self, patience=100): self.patience = patience self.best_valid = np.inf self.best_valid_epoch = 0 self.best_weights = None def __call__(self, nn, train_history): current_valid = train_history[-1]['valid_loss'] current_epoch = train_history[-1]['epoch'] if current_valid < self.best_valid: self.best_valid = current_valid self.best_valid_epoch = current_epoch self.best_weights = nn.get_all_params_values() elif self.best_valid_epoch + self.patience < current_epoch: print("Early stopping.") print("Best valid loss was {:.6f} at epoch {}.".format( self.best_valid, self.best_valid_epoch)) nn.load_params_from(self.best_weights) raise StopIteration()

你可以看到在__call__内部有两个分支：第一个是当前验证分数优于之前看到的情况，第二个是最佳验证时期比self.patience个时期之前。在第一种情况下，我们存储权重：

self.best_weights = nn.get_all_params_values()

在第二种情况下，我们将网络的权重设置回到那些最佳权重，然后引发StopIteration，向神经网络发出我们要停止训练的信号。

nn.load_params_from(self.best_weights) raise StopIteration()

让我们更新网络定义中的 on_epoch_finished 处理程序列表，并使用 EarlyStopping：

net8
= NeuralNet(
\

... on_epoch_finished=

[ AdjustVariable('update_learning_rate', start=0.03, stop=0.0001), AdjustVariable('update_momentum', start=0.9, stop=0.999), EarlyStopping(patience=200), ], \

... )

迄今为止一切顺利，但我们该如何定义这些专家以及他们应该预测什么？让我们为此制定一个清单：

SPECIALIST_SETTINGS = [ dict( columns=('left_eye_center_x', 'left_eye_center_y', 'right_eye_center_x', 'right_eye_center_y', ), flip_indices=((0, 2), (1, 3)), ), dict( columns=('nose_tip_x', 'nose_tip_y', ), flip_indices=(), ), dict( columns=('mouth_left_corner_x', 'mouth_left_corner_y', 'mouth_right_corner_x', 'mouth_right_corner_y', 'mouth_center_top_lip_x', 'mouth_center_top_lip_y', ), flip_indices=((0, 2), (1, 3)), ), dict( columns=('mouth_center_bottom_lip_x', 'mouth_center_bottom_lip_y', ), flip_indices=(), ), dict( columns=('left_eye_inner_corner_x', 'left_eye_inner_corner_y', 'right_eye_inner_corner_x', 'right_eye_inner_corner_y', 'left_eye_outer_corner_x', 'left_eye_outer_corner_y', 'right_eye_outer_corner_x', 'right_eye_outer_corner_y', ), flip_indices=((0, 2), (1, 3), (4, 6), (5, 7)), ), dict( columns=('left_eyebrow_inner_end_x', 'left_eyebrow_inner_end_y', 'right_eyebrow_inner_end_x', 'right_eyebrow_inner_end_y', 'left_eyebrow_outer_end_x', 'left_eyebrow_outer_end_y', 'right_eyebrow_outer_end_x', 'right_eyebrow_outer_end_y', ), flip_indices=((0, 2), (1, 3), (4, 6), (5, 7)), ), ]

我们已经讨论过在数据增强部分中需要flip_indices。从数据部分记得，我们的load_data()函数接受一个可选的列提取列表。当我们在新函数fit_specialists()中拟合专家模型时，我们将利用这个特性：

from collections import OrderedDict from sklearn.base import clone def fit_specialists(): specialists = OrderedDict() for setting in SPECIALIST_SETTINGS: cols = setting['columns'] X, y = load2d(cols=cols) model = clone(net) model.output_num_units = y.shape[1] model.batch_iterator_train.flip_indices = setting['flip_indices'] # set number of epochs relative to number of training examples: model.max_epochs = int(1e7 / y.shape[0]) if 'kwargs' in setting: # an option 'kwargs' in the settings list may be used to # set any other parameter of the net: vars(model).update(setting['kwargs']) print("Training model for columns {} for {} epochs".format(cols, model.max_epochs)) model.fit(X, y) specialists[cols] = model with open('net-specialists.pickle', 'wb') as f: # we persist a dictionary with all models: pickle.dump(specialists, f, -1)

这里没有什么特别惊人的事情发生。我们不是训练和持久化单个模型，而是使用保存在字典中的模型列表，将列映射到训练好的 NeuralNet 实例。尽管我们采用了提前停止策略，但这仍然需要很长时间来训练（尽管我说的不是Google-forever，而是可能需要在单个 GPU 上花费半天时间）；我不建议您真的运行这个。

当然，我们可以很容易地在多个GPU上并行训练这些专家网络，但也许您没有多个CUDA GPU的访问权限。在下一节中，我们将讨论另一种缩短训练时间的方法。但首先让我们看看拟合这些昂贵的专家网络的结果：

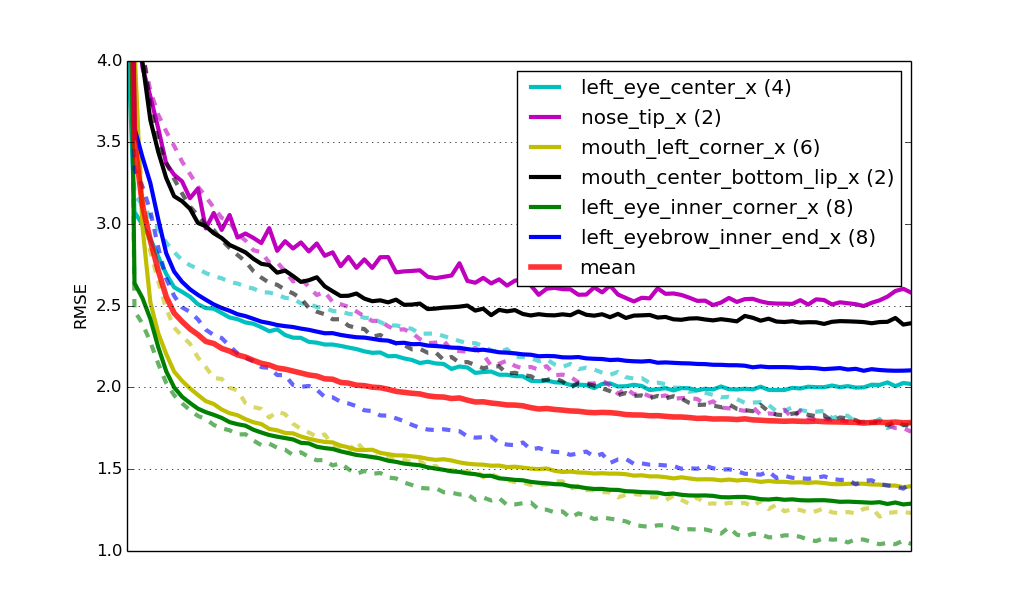
六个专业模型的学习曲线。实线代表验证集上的RMSE，虚线代表训练集上的误差。mean是所有网络的加权目标值数量的平均验证误差。所有曲线已经按照x轴长度进行了缩放。

最后，这个解决方案给我们带来了一个Kaggle排行榜得分为2.17 RMSE，在撰写时排名第二（紧随在您的后面）。

在本教程的最后一部分，我们将讨论一种使专家训练更快的方法。这个想法是：不再随机初始化每个专家网络的权重，而是使用在net6或net7中学习到的权重进行初始化。从我们的EarlyStopping实现中记得，将一个网络的权重复制到另一个网络就像使用load_params_from()方法那样简单。让我们修改fit_specialists方法来实现这一点。我再次用# !注释标记与之前实现相比发生变化的行：

def fit_specialists(fname_pretrain=None): if fname_pretrain:

with open(fname_pretrain, 'rb') as f: 
    net_pretrain = pickle.load(f) 

else: net_pretrain = None

specialists = OrderedDict() for setting in SPECIALIST_SETTINGS: cols = setting['columns'] X, y = load2d(cols=cols) model = clone(net) model.output_num_units = y.shape[1] model.batch_iterator_train.flip_indices = setting['flip_indices'] model.max_epochs = int(4e6 / y.shape[0]) if 'kwargs' in setting: vars(model).update(setting['kwargs']) if net_pretrain is not None: model.load_params_from(net_pretrain) print("Training model for columns {} for {} epochs".format(cols, model.max_epochs)) model.fit(X, y) specialists[cols] = model

with open('net-specialists.pickle', 'wb') as f: pickle.dump(specialists, f, -1)

初始化这些网络时不是随机的，而是通过重复使用我们之前学习的网络中的权重，事实上有两个重大优势：一是训练收敛速度更快；在这种情况下可能快四倍。第二个优势是它还有助于获得更好的泛化能力；预训练起到了正则化的作用。这是与之前相同的学习曲线，但现在是针对预训练网络的。

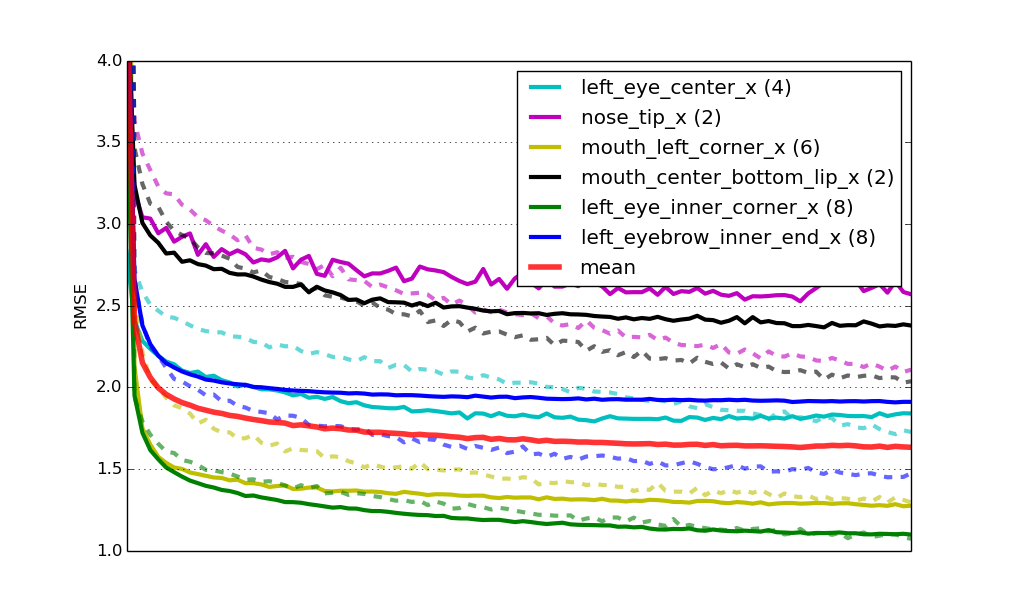
六个预训练专业模型的学习曲线。

最终，在挑战排行榜上，这个解决方案的得分为2.13均方根误差。再次获得第二名，但已经越来越接近了！

你可能有十几个想尝试的想法。你可以在这里找到最终解决方案的源代码进行下载和尝试。它还包括生成Kaggle挑战提交文件的部分。运行 python kfkd.py 以了解如何在命令行上使用该脚本。

这里有一些更明显的事情，你可以尝试一下：尝试优化各个专家网络的参数；这是我们到目前为止还没有做过的事情。注意我们训练的六个网络都有不同程度的过拟合。如果像上面的绿色和黄色网络一样没有或几乎没有过拟合，你可以尝试减少dropout的数量。同样，如果像黑色和紫色网络那样过拟合严重，你可以尝试增加dropout的数量。在SPECIALIST_SETTINGS的定义中，我们已经可以添加一些特定于网络的设置；比如说，如果我们想要给第二个网络增加更多的正则化，那么我们可以将列表的第二个条目更改为如下所示：

dict(columns tip_x', 'nose_tip_y', ), flip_indices=(), kwargs=dict(dropout2_p=0.3, dropout3_p=0.4), )

还有很多其他可以尝试调整的东西。也许你会尝试添加另一个卷积层或全连接层？我很想听听你在评论中能够想出的改进。

编辑: Kaggle 在他们的网站上展示了这个教程，其中包括如何使用亚马逊GPU实例来运行教程的说明，如果你没有拥有CUDA兼容的GPU，这将非常有用。