在我的介绍性文章中,我讨论了各种模型(欠完备、稀疏、去噪、收缩),这些模型将数据作为输入,并发现该数据的一些潜在状态表示。更具体地说,我们的输入数据被转换为一个_编码向量_,其中每个维度代表关于数据的一些学习属性。这里最重要的细节是,我们的编码器网络为每个编码维度输出一个_单个值_。然后解码器网络随后获取这些值,并尝试重新创建原始输入。
变分自编码器(VAE)提供了一种用概率描述潜在空间中观察的方式。因此,我们不是构建一个输出单个值来描述每个潜在状态属性的编码器,而是设计我们的编码器来描述每个潜在属性的概率分布。
直觉
举个例子,假设我们已经在一个包含大量人脸数据集的自编码器模型上进行了训练,编码维度为6。理想的自编码器将学习人脸的描述性属性,比如肤色、人是否戴眼镜等,试图用一种压缩表示来描述观察结果。
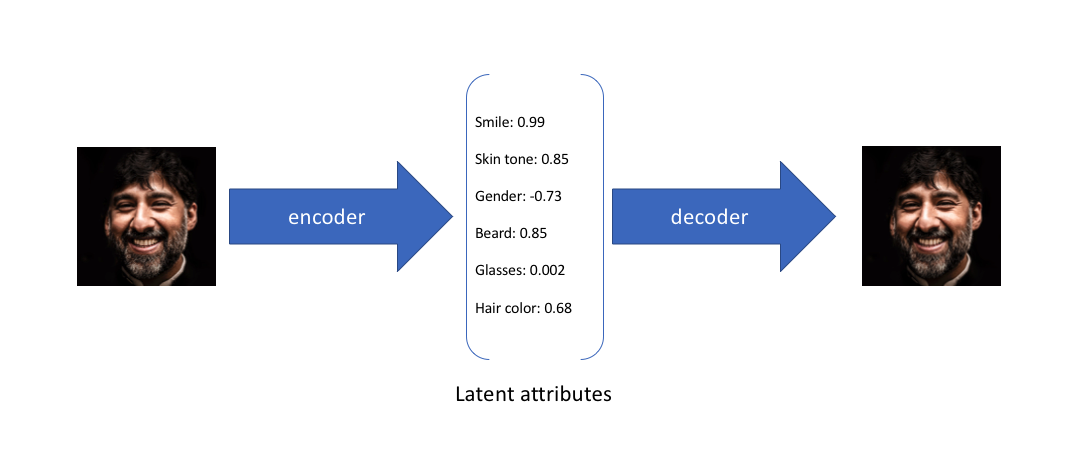
在上面的示例中,我们已经用单个值描述了输入图像的潜在属性。然而,我们可能更喜欢将每个潜在属性表示为一系列可能的值。例如,如果您输入蒙娜丽莎的照片,您会为微笑属性分配什么 单个值?使用变分自动编码器,我们可以用概率术语描述潜在属性。
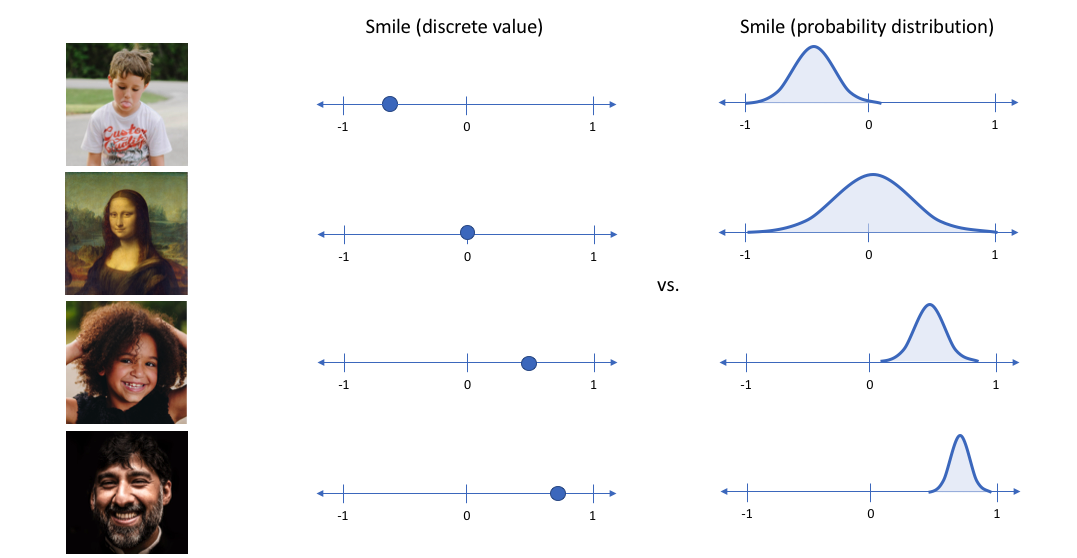
通过这种方法,我们现在将为给定输入表示为概率分布的每个潜在属性。在从潜在状态解码时,我们将从每个潜在状态分布中随机抽样,以生成一个向量作为我们解码器模型的输入。
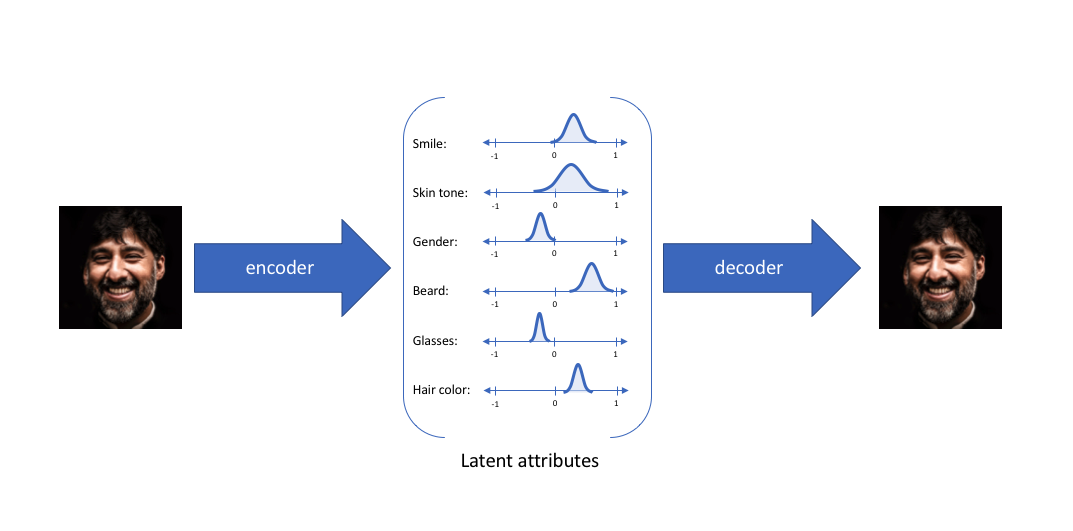
注意:对于变分自动编码器,编码器模型有时被称为识别模型,而解码器模型有时被称为生成模型。
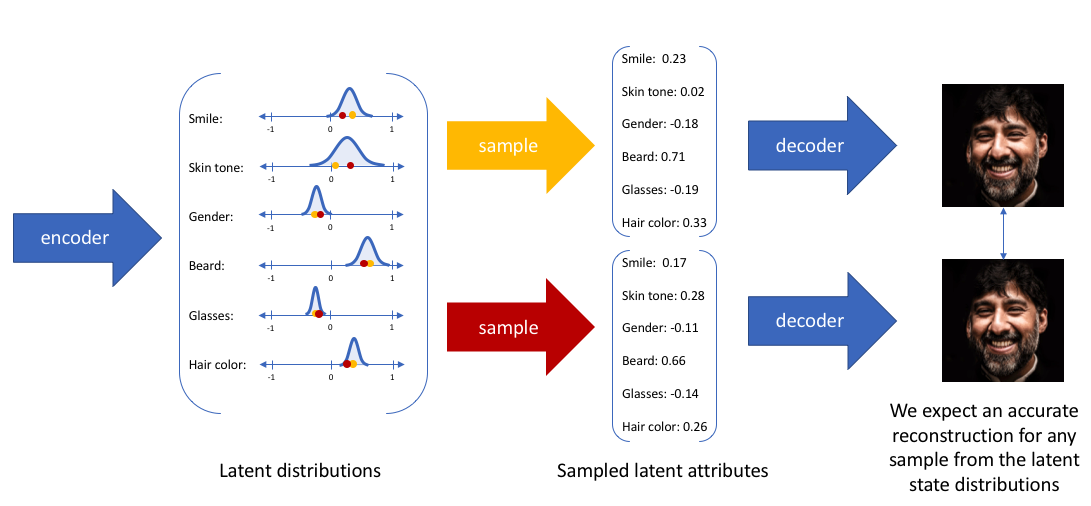
通过构建我们的编码器模型,使其输出一系列可能的值(一个统计分布),我们将随机抽样以输入解码器模型,从而实质上强制实现连续、平滑的潜在空间表示。对于潜在分布的任何抽样,我们期望我们的解码器模型能够准确重构输入。因此,在潜在空间中彼此相邻的值应该对应非常相似的重构。
统计动机
假设存在某个隐藏变量生成了一个观测值。
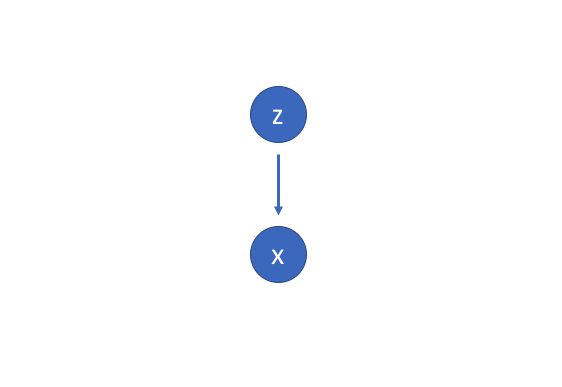
我们只能看到,但我们想推断其特征。换句话说,我们想计算。
不幸的是,计算是相当困难的。
让我们通过另一个分布来近似,我们将定义这个分布,使其成为一个易处理的分布。如果我们能够定义参数,使其与非易处理分布非常相似,我们就可以使用它来执行近似推断。
回想一下KL散度是两个概率分布之间差异的度量。因此,如果我们想要确保与 相似,我们可以最小化两个分布之间的KL散度。
Dr. Ali Ghodsi在这里进行了完整的推导,但结果告诉我们,通过最大化以下内容,我们可以最小化上述表达式:
第一项代表重建似然性,第二项确保我们学习到的分布类似于真实的先验分布。
重新审视我们的图形模型,我们可以使用来推断可能的隐藏变量(即潜在状态),这些变量被用来生成观察结果。我们可以进一步将这个模型构建成一个神经网络架构,其中编码器模型学习从到的映射,解码器模型学习从回到的映射。
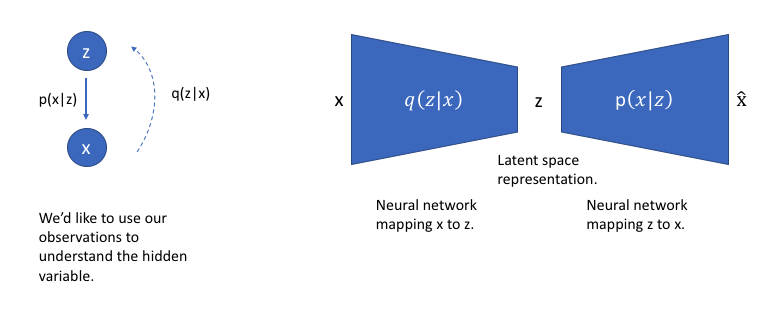
我们这个网络的损失函数将由两个项组成,一个惩罚重构误差(可以理解为最大化重构似然性,如前所述),另一个鼓励我们学习到的分布与真实的先验分布相似,我们假设真实的先验分布是单位高斯分布,对于潜在空间的每个维度。
实施
在前一节中,我为变分自动编码器结构建立了统计动机。在本节中,我将提供构建这样一个模型的实际实现细节。
与标准自动编码器直接输出潜在状态值不同,VAE的编码器模型将为潜在空间中的每个维度输出描述分布的参数。由于我们假设先验遵循正态分布,我们将输出 两个 描述潜在状态分布均值和方差的向量。如果我们要构建一个真正的多元高斯模型,我们需要定义一个协方差矩阵,描述每个维度之间的相关性。然而,我们将做一个简化假设,即我们的协方差矩阵只在对角线上有非零值,这样我们可以用一个简单的向量描述这些信息。
我们的解码模型将通过从这些定义的分布中进行采样来生成一个潜在向量,然后继续开发原始输入的重建。
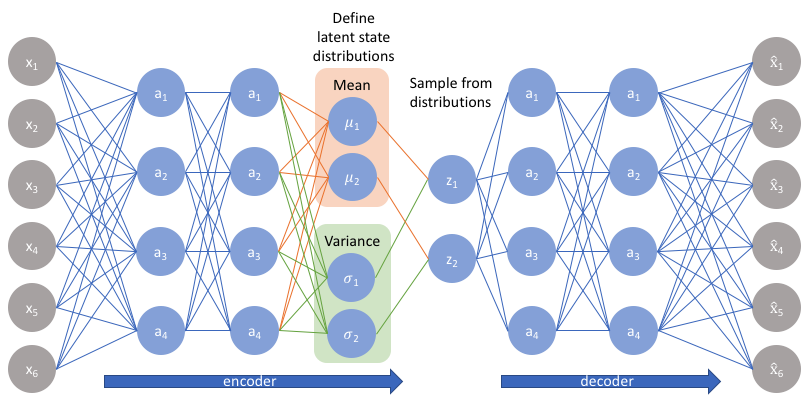
然而,这种采样过程需要额外注意。在训练模型时,我们需要能够使用一种称为反向传播的技术来计算网络中每个参数与最终输出损失之间的关系。然而,我们无法简单地对随机采样过程执行此操作。幸运的是,我们可以利用一种称为“重新参数化技巧”的巧妙想法,该想法建议我们从单位高斯中随机采样,然后通过潜在分布的均值进行偏移,并通过潜在分布的方差进行缩放。
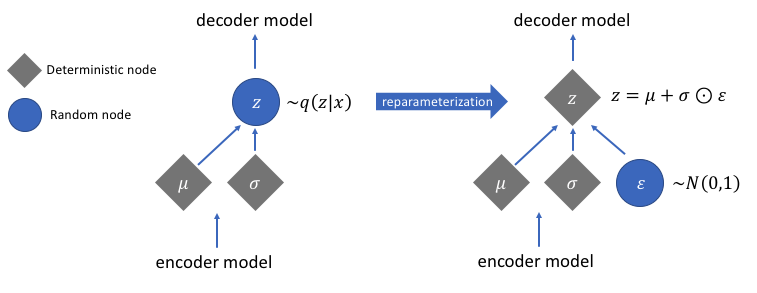
通过这种重新参数化,我们现在可以优化分布的 参数,同时仍然保持从该分布中随机抽样的能力。
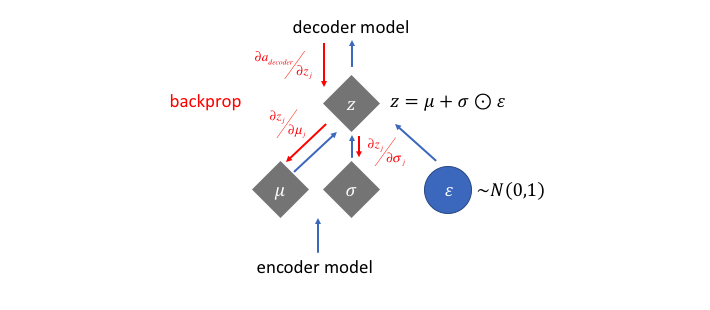
注意:为了处理网络可能学习到的 负值,通常会让网络学习 并对该值进行指数运算,以获得潜在分布的方差。
潜空间的可视化
要理解变分自动编码器模型的含义以及它与标准自动编码器架构的区别,检查潜在空间是很有用的。这篇博客文章介绍了这个主题的深入讨论,我将在本节中进行总结。
变分自动编码器的主要优点在于我们能够学习输入数据的平滑潜在状态表示。对于标准自动编码器,我们只需要学习一种编码,使我们能够重现输入。正如您在最左边的图中所看到的,仅关注重构损失确实可以让我们分离出类别(在本例中是MNIST数字),这应该让我们的解码器模型能够重现原始手写数字,但潜在空间中的数据分布不均匀。换句话说,潜在空间中存在一些区域,这些区域不代表我们观察到的任何数据。
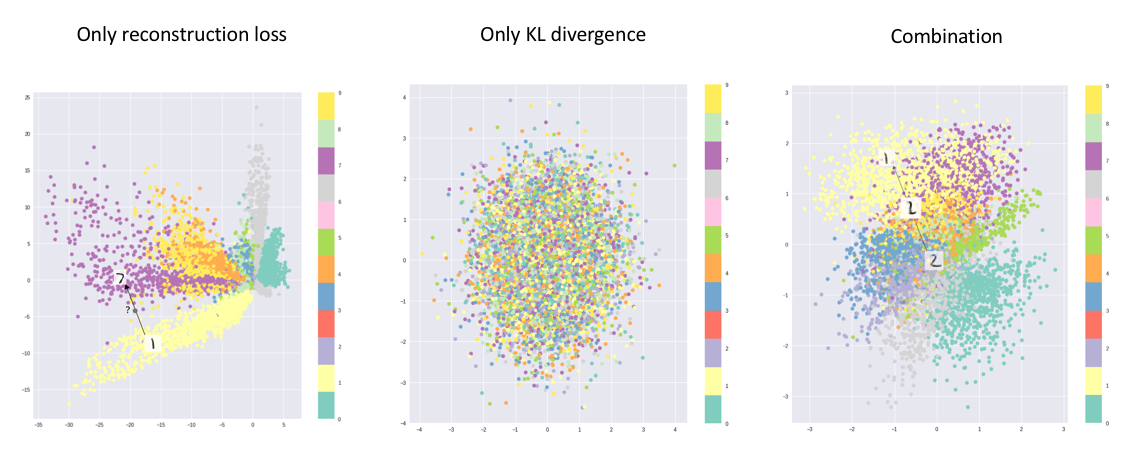
Image credit (modified)
另一方面,如果我们只关注确保潜在分布类似于先验分布(通过KL散度损失项),我们最终会用相同的单位高斯来描述每个观测值,然后我们从中采样以描述可视化的潜在维度。这实际上将每个观测视为具有相同的特征;换句话说,我们未能描述原始数据。
然而,当同时优化这两个术语时,我们被鼓励用分布来描述观察的潜在状态,这些分布与先验分布接近,但在必要时会偏离以描述输入的显著特征。
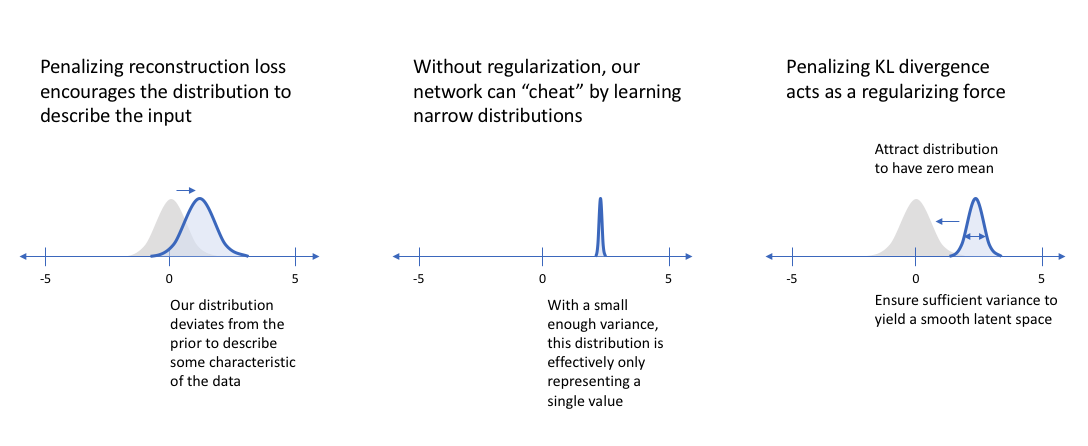
当我构建变分自动编码器时,我喜欢检查数据中几个样本的潜在维度,以了解分布的特征。我鼓励你也这样做。
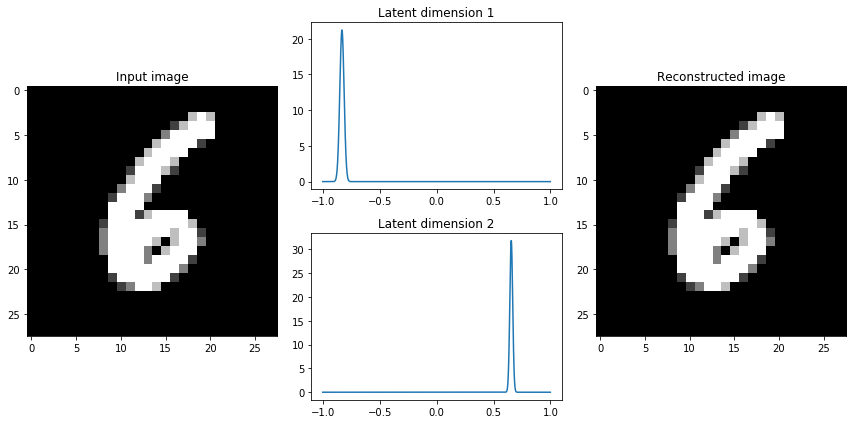
如果我们观察到潜在分布非常紧凑,我们可能决定给KL散度项更高的权重,使用一个参数,鼓励网络学习更广泛的分布。这个简单的洞察导致了一类新模型的发展 - 解缠变分自动编码器。事实证明,通过更加强调KL散度项,我们也在隐式地强制学习到的潜在维度是不相关的(通过我们对对角协方差矩阵的简化假设)。
变分自动编码器作为生成模型
通过从潜在空间进行采样,我们可以使用解码器网络构建一个生成模型,能够创建类似于训练期间观察到的新数据。具体来说,我们将从先验分布中进行采样,我们假设该分布遵循单位高斯分布。
下图可视化了在MNIST手写数字数据集上训练的变分自动编码器的解码器网络生成的数据。在这里,我们从二维高斯中采样了一组值,并显示了我们解码器网络的输出。

正如您所看到的,不同的数字存在于潜在空间的不同区域,并且可以平滑地从一个数字转换为另一个数字。当您希望在两个观察值之间进行插值时,这种平滑转换非常有用,比如最近的一个例子是Google构建了一个模型,用于在两个音乐样本之间进行插值。
进一步阅读
讲座
博客/视频
论文/书籍
我阅读列表上的论文