Autoencoders 是一种无监督学习技术,其中我们利用神经网络来进行表示学习任务。具体来说,我们将设计一个神经网络架构,通过在网络中强制施加一个瓶颈,从而迫使对原始输入进行压缩知识表示。如果输入特征彼此独立,这种压缩和后续重建将是一项非常困难的任务。然而,如果数据中存在某种结构(即输入特征之间的相关性),这种结构可以被学习,从而在强制输入通过网络的瓶颈时得到利用。
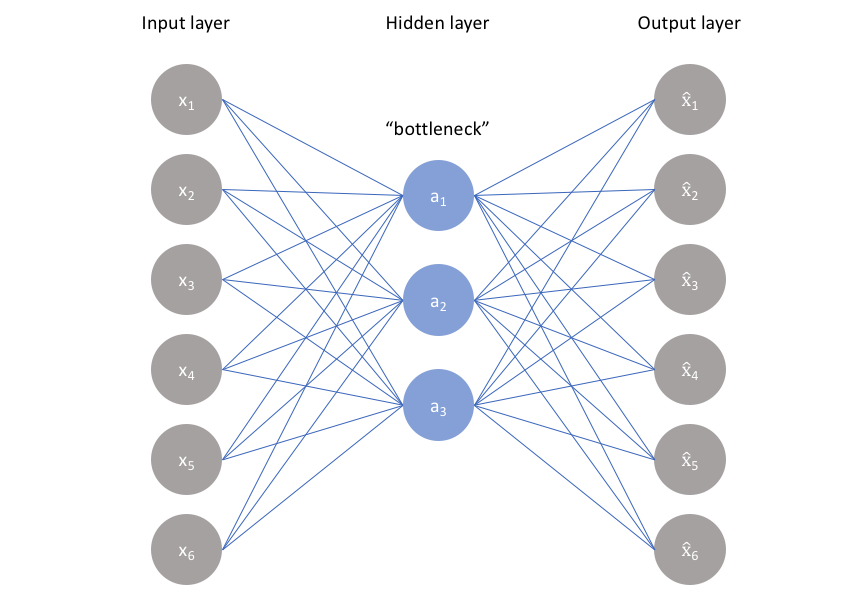
如上图所示,我们可以将一个未标记的数据集构建成一个监督学习问题,其任务是输出原始输入的重构。通过最小化_重构误差_来训练这个网络,该误差衡量了原始输入与后续重构之间的差异。瓶颈是我们网络设计的一个关键属性;如果没有信息瓶颈的存在,我们的网络很容易学会简单地通过网络传递这些值来记忆输入值(如下图所示)。
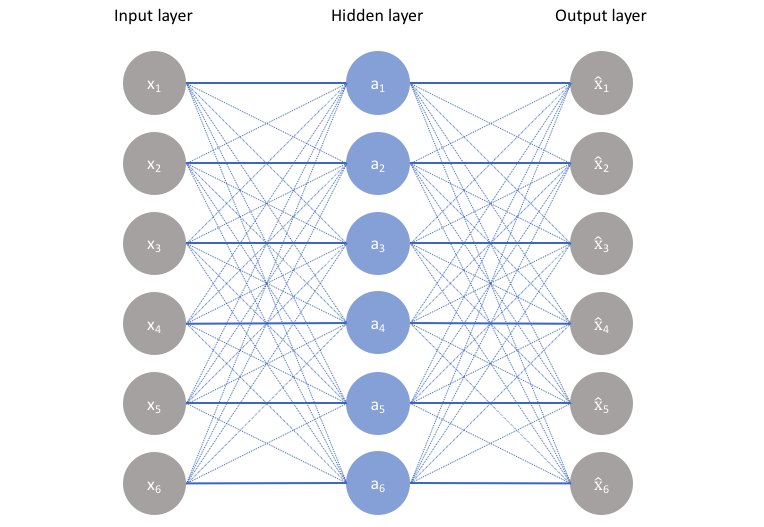
瓶颈限制了可以在整个网络中传输的信息量,迫使对输入数据进行学习压缩。
注意:实际上,如果我们构建一个线性网络(即在每一层不使用非线性激活函数),我们会观察到与PCA中观察到的类似的降维。请参阅 Geoffrey Hinton 在此处的讨论。
理想的自动编码器模型平衡以下内容:
- 对输入敏感到足以准确构建重建。
- 对输入不敏感到足以使模型不会简单地记忆或过度拟合训练数据。
这种权衡迫使模型仅保留数据中重建输入所需的变化,而不保留输入中的冗余。在大多数情况下,这涉及构建一个损失函数,其中一个项鼓励我们的模型对输入敏感(即重建损失),另一个项阻止记忆/过拟合(即添加的正则化项)。
通常我们会在正则化项前面添加一个缩放参数,这样我们就可以调整两个目标之间的权衡。
在这篇文章中,我将讨论一些用于施加这两个约束并调整权衡的标准自动编码器架构;在后续的文章中,我将讨论变分自动编码器,它基于这里讨论的概念构建一个更强大的模型。
欠完备自编码器
构建自动编码器的最简单架构是限制网络隐藏层中节点的数量,从而限制信息在网络中传递的数量。通过根据重构误差对网络进行惩罚,我们的模型可以学习输入数据的最重要属性,以及如何最佳地从“编码”状态重构原始输入。理想情况下,这种编码将学习并描述输入数据的潜在属性。
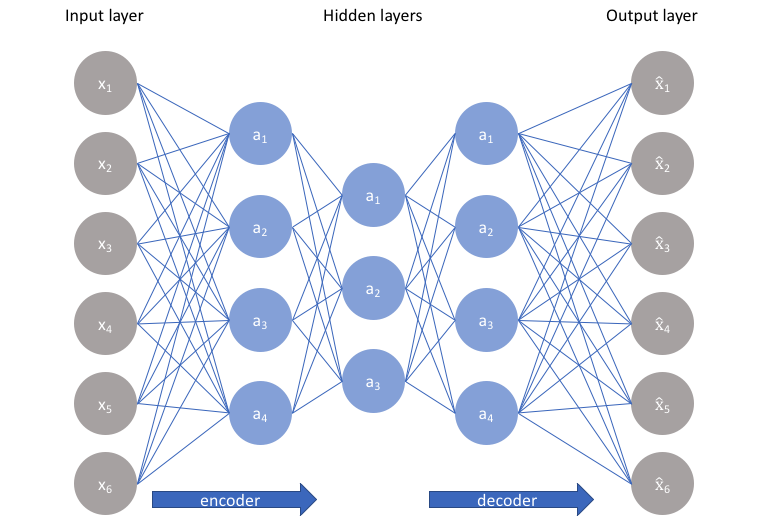
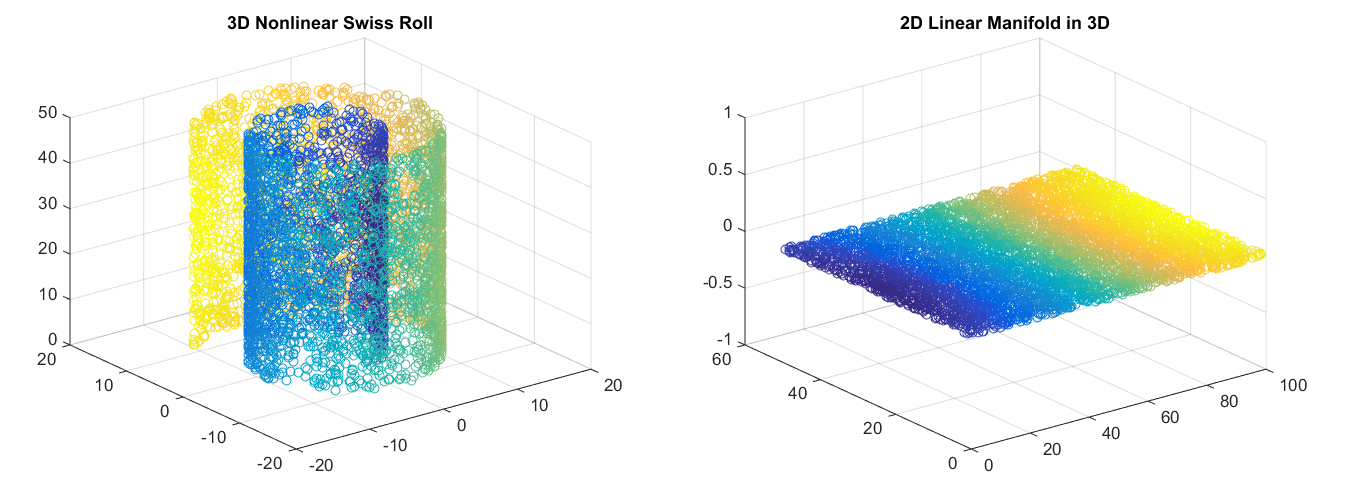
因为神经网络能够学习非线性关系,这可以被视为对PCA的更强大(非线性)泛化。而PCA试图发现描述原始数据的低维超平面,自编码器则能够学习非线性流形(流形在简单的术语中被定义为连续、不相交的表面)。这两种方法之间的差异如下图所示。
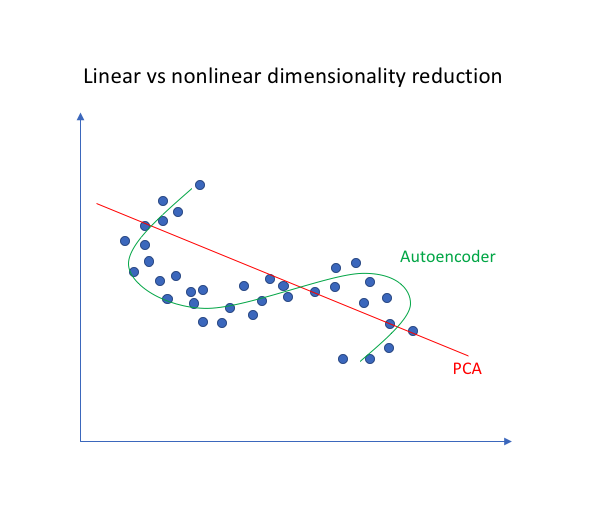
对于更高维度的数据,自动编码器能够学习数据的复杂表示(流形),这可以用来描述较低维度中的观测结果,并相应地解码为原始输入空间。
一个欠完备自编码器没有显式的正则化项 - 我们只是根据重构损失训练我们的模型。因此,确保模型没有记忆输入数据的唯一方法是确保我们已经充分限制了隐藏层中节点的数量。
对于深度自动编码器,我们还必须意识到我们编码器和解码器模型的_容量_。即使“瓶颈层”只有一个隐藏节点,只要编码器和解码器模型具有足够的能力学习一些任意函数,可以将数据映射到索引,我们的模型仍然有可能记住训练数据。
考虑到我们希望模型能够发现数据中的潜在属性,确保自动编码器模型不仅仅是在学习有效地记忆训练数据是非常重要的。与监督学习问题类似,我们可以采用各种形式的正则化技术来鼓励网络具有良好的泛化性能;下面将讨论这些技术。
稀疏自编码器
稀疏自编码器为我们提供了一种替代方法,可以引入信息瓶颈,而无需在隐藏层节点数量上进行减少。相反,我们将构建损失函数,以惩罚层内的激活。对于任何给定的观察,我们将鼓励网络学习一种编码和解码,只依赖于激活少量的神经元。值得注意的是,这是一种不同的正则化方法,因为我们通常对网络的权重进行正则化,而不是激活。
下面展示了一个通用的稀疏自动编码器,其中节点的不透明度与激活水平相对应。重要的是要注意,训练模型的各个节点激活是_数据相关的_,不同的输入将导致网络中不同节点的激活。
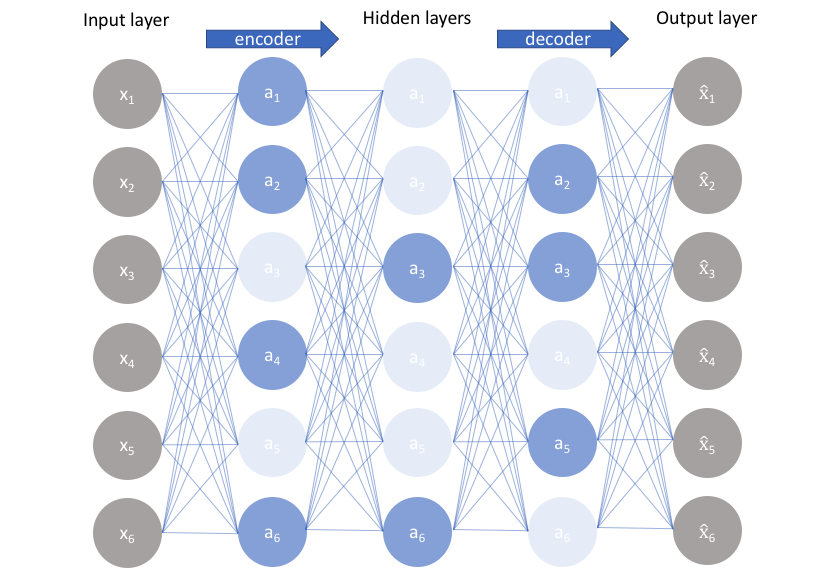
这一事实的一个结果是我们允许网络使得每个隐藏层节点对输入数据的特定属性变得敏感。相比之下,欠完备自编码器会对每个观测使用整个网络,而稀疏自编码器将被迫根据输入数据有选择性地激活网络的不同区域。因此,我们限制了网络记忆输入数据的能力,同时又不限制网络从数据中提取特征的能力。这使我们能够将网络的潜在状态表示和正则化_分开_考虑,从而我们可以根据数据的上下文选择潜在状态表示(即编码维度),同时通过稀疏约束施加正则化。
有两种主要方法可以施加这种稀疏性约束;两种方法都涉及测量每个训练批次的隐藏层激活,并在损失函数中添加一些项,以惩罚过度激活。这些项是:
- L1正则化: 我们可以在损失函数中添加一个项,惩罚观测中层激活向量的绝对值,乘以一个调节参数进行缩放。
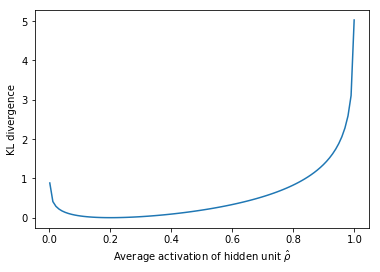
- KL散度: 本质上,KL散度是衡量两个概率分布之间差异的指标。我们可以定义一个稀疏度参数,表示神经元在一组样本中的平均激活。这个期望可以计算为,其中下标表示层中特定的神经元,对训练观测的激活求和,分别表示为。本质上,通过约束神经元在一组样本中的平均激活,我们鼓励神经元仅对一部分观测进行激活。我们可以将描述为伯努利随机变量分布,从而利用KL散度(下面展开)比较理想分布与所有隐藏层节点上观察到的分布。
注意:伯努利分布 是“随机变量取值为1的概率为 ,取值为0的概率为 ”的概率分布。这与建立神经元将发放的概率相当吻合。
两个伯努利分布之间的KL散度可以写成。这个损失项在下面的图中可视化,对应于这一点的最小(零)惩罚。
降噪自编码器
到目前为止,我已经讨论了训练神经网络的概念,其中输入和输出是相同的,我们的模型的任务是尽可能地复制输入,同时通过某种信息瓶颈。回想一下,我提到我们希望我们的自动编码器足够敏感,以重新创建原始观察结果,但又不够敏感以至于模型学习到可泛化的编码和解码。开发可泛化模型的另一种方法是轻微破坏输入数据,但仍保持未破坏的数据作为我们的目标输出。
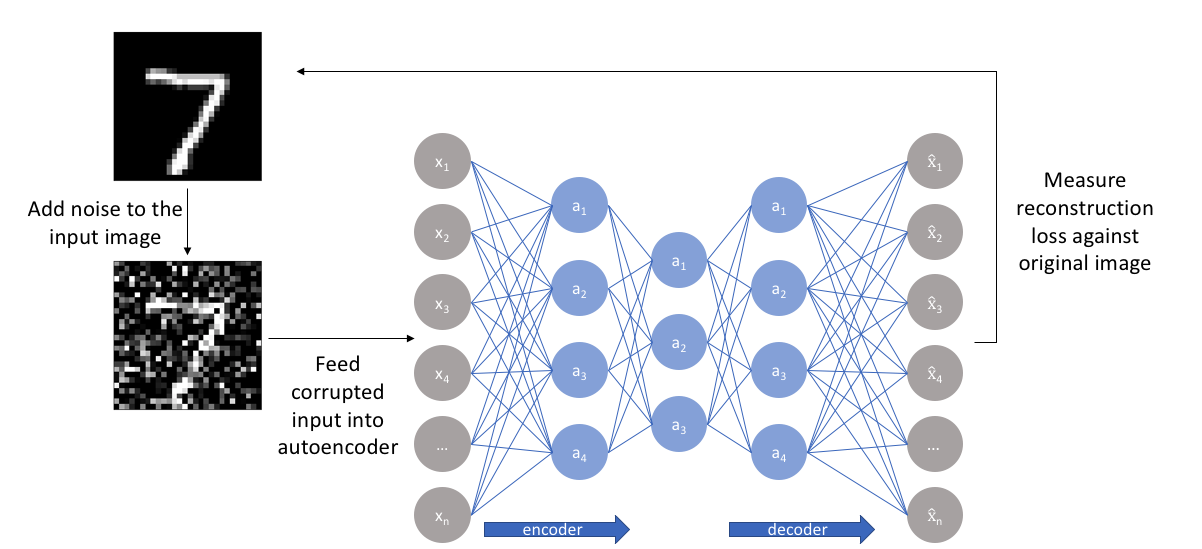
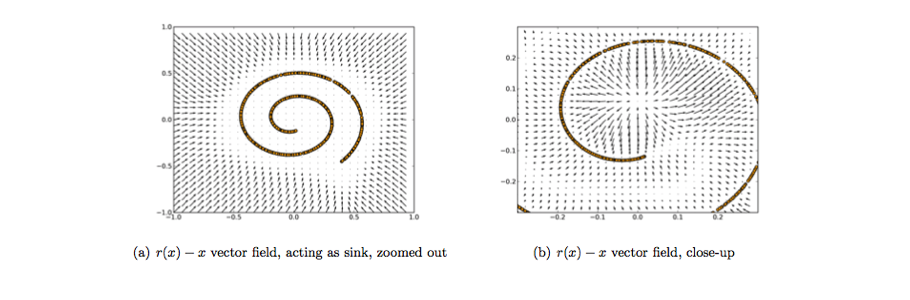
采用这种方法,我们的模型无法简单地开发一个映射,记住训练数据,因为我们的输入和目标输出不再相同。相反,模型学习了一个矢量场,将输入数据映射到一个低维流形(回想一下我之前的图形,流形描述了输入数据集中的高密度区域);如果这个流形准确描述了自然数据,我们有效地“抵消”了添加的噪音。
上图可视化了通过将 的重建与原始值进行比较所描述的向量场。黄色点表示在添加噪音之前的训练示例。正如您所看到的,模型已经学会将受损输入调整到学习到的流形。
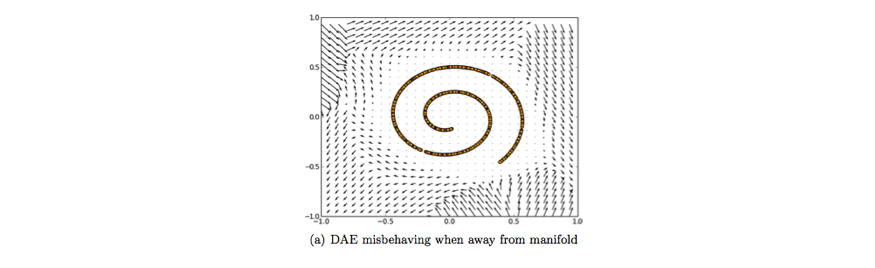
值得注意的是,这个向量场通常只在模型在训练期间观察到的区域内表现良好。在远离自然数据分布的区域,重建误差通常较大,并且并不总是指向真实分布的方向。
压缩自编码器
人们会期望,对于非常相似的输入,学习到的编码也会非常相似。我们可以明确地训练我们的模型,以便这种情况发生,要求隐藏层激活的导数对输入很小。换句话说,对输入进行微小更改时,我们仍应保持非常相似的编码状态。这与去噪自编码器非常相似,因为这些对输入的微小扰动本质上被视为噪声,我们希望我们的模型对噪声具有鲁棒性。换句话说,"去噪自编码器使重构函数(即解码器)抵抗输入的微小但有限大小的扰动,而收缩自编码器使特征提取函数(即编码器)抵抗输入的无穷小扰动。"
因为我们明确地鼓励我们的模型学习一种编码方式,其中相似的输入具有相似的编码,我们实质上是在强迫模型学习如何将输入的邻域收缩为输出的较小邻域。请注意,对于输入数据的局部邻域,重构数据的斜率(即导数)基本上为零。
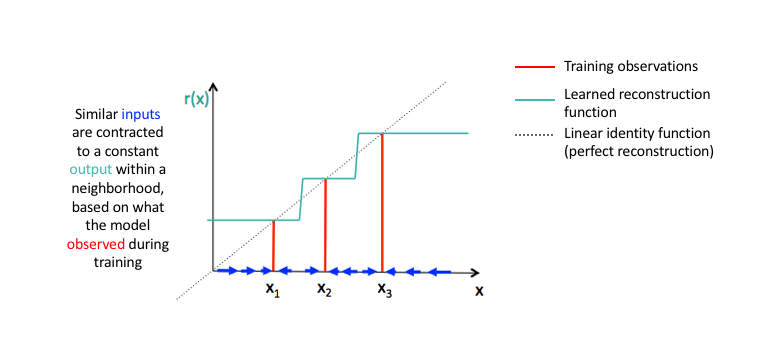
Image credit (modified)
我们可以通过构建一个损失项来实现这一点,该损失项惩罚我们的隐藏层激活相对于输入训练示例的大导数,从本质上惩罚输入的微小变化导致编码空间的大变化的情况。
在更高级的数学术语中,我们可以将正则化损失项构建为对于输入观测值的隐藏层激活的雅可比矩阵的Frobenius范数的平方。Frobenius范数本质上是矩阵的L2范数,而雅可比矩阵简单地表示了向量值函数的所有一阶偏导数(在这种情况下,我们有一个训练样本的向量)。
对于观测值和隐藏层节点,我们可以按以下方式计算这些值。
更简洁地表达,我们可以将完整的损失函数定义为
定义了关于输入的隐藏层激活的梯度场,对所有训练示例求和。
摘要
自动编码器是一种神经网络架构,能够发现数据中的结构,以开发输入的压缩表示。存在许多不同变体的通用自动编码器架构,旨在确保压缩表示代表原始数据输入的有意义属性;通常在使用自动编码器时最大的挑战是让模型真正学习到有意义且可泛化的潜在空间表示。
因为自动编码器根据属性(即输入特征向量之间的相关性)在训练期间从数据中发现,学习如何压缩数据,所以这些模型通常只能重建与模型在训练期间观察到的观测类似的数据。
自动编码器的应用包括:
- 异常检测
- 数据去噪(例如图像、音频)
- 图像修复
- 信息检索
进一步阅读
讲座/笔记
博客/视频
论文/书籍