NumPy Array is the foundation of numerical computing in Python. These powerful data structures provide a fast and efficient way to work with large datasets, perform mathematical operations, and analyze complex data. In this comprehensive guide, we’ll explore the ins and outs of NumPy Array, from basic creation and manipulation to advanced techniques and applications.
Numpy Array Recommended Articles
Introduction to NumPy Array
NumPy Array are the core data structure of the NumPy library, which is essential for scientific computing in Python. Unlike Python lists, NumPy Array are homogeneous, meaning they contain elements of the same data type. This uniformity allows for faster computations and more efficient memory usage.
Let’s start with a simple example of creating a NumPy array:
import numpy as np
# Create a 1D NumPy array
arr = np.array([1, 2, 3, 4, 5])
print("numpyarray.com - 1D array:", arr)
Output:

In this example, we import NumPy and create a one-dimensional array using the np.array() function. The resulting array contains integers and can be easily manipulated using various NumPy functions.
Creating NumPy Array
There are multiple ways to create NumPy Array, each suited for different scenarios. Let’s explore some common methods:
Using np.array()
The most straightforward way to create a NumPy array is by using the np.array() function:
import numpy as np
# Create a 2D NumPy array
arr_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print("numpyarray.com - 2D array:")
print(arr_2d)
Output:

This example creates a 2D array from a list of lists. NumPy automatically determines the shape of the array based on the input.
Using np.zeros() and np.ones()
To create arrays filled with zeros or ones, you can use np.zeros() and np.ones():
import numpy as np
# Create an array of zeros
zeros_arr = np.zeros((3, 4))
print("numpyarray.com - Array of zeros:")
print(zeros_arr)
# Create an array of ones
ones_arr = np.ones((2, 3, 2))
print("numpyarray.com - Array of ones:")
print(ones_arr)
Output:

These functions take a tuple specifying the shape of the array as an argument. The resulting arrays are filled with floating-point zeros or ones by default.
Using np.arange() and np.linspace()
For creating arrays with evenly spaced values, np.arange() and np.linspace() are useful:
import numpy as np
# Create an array with evenly spaced values using arange
arange_arr = np.arange(0, 10, 2)
print("numpyarray.com - Array created with arange:", arange_arr)
# Create an array with evenly spaced values using linspace
linspace_arr = np.linspace(0, 1, 5)
print("numpyarray.com - Array created with linspace:", linspace_arr)
Output:

np.arange() creates an array with values from 0 to 10 (exclusive) with a step of 2, while np.linspace() creates an array of 5 evenly spaced values between 0 and 1 (inclusive).
Array Attributes and Properties
NumPy Array has several attributes and properties that provide useful information about their structure and content. Let’s explore some of the most important ones:
Shape and Size
The shape attribute returns a tuple representing the dimensions of the array, while size gives the total number of elements:
import numpy as np
arr = np.array([[1, 2, 3], [4, 5, 6]])
print("numpyarray.com - Array shape:", arr.shape)
print("numpyarray.com - Array size:", arr.size)
Output:

In this example, we create a 2D array and print its shape (2 rows, 3 columns) and size (6 elements).
Data Type
The dtype attribute provides information about the data type of the array elements:
import numpy as np
arr_int = np.array([1, 2, 3])
arr_float = np.array([1.0, 2.0, 3.0])
print("numpyarray.com - Integer array dtype:", arr_int.dtype)
print("numpyarray.com - Float array dtype:", arr_float.dtype)
Output:

This example demonstrates how NumPy automatically determines the appropriate data type for the array based on its contents.
Dimensions
The ndim attribute returns the number of dimensions (axes) of the array:
import numpy as np
arr_1d = np.array([1, 2, 3])
arr_2d = np.array([[1, 2], [3, 4]])
arr_3d = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
print("numpyarray.com - 1D array ndim:", arr_1d.ndim)
print("numpyarray.com - 2D array ndim:", arr_2d.ndim)
print("numpyarray.com - 3D array ndim:", arr_3d.ndim)
Output:

This example shows how to determine the number of dimensions for arrays of different ranks.
Indexing and Slicing NumPy Array
Efficient data access and manipulation are crucial when working with NumPy Array. Let’s explore various indexing and slicing techniques:
Basic Indexing
NumPy Array supports integer indexing similar to Python lists:
import numpy as np
arr = np.array([10, 20, 30, 40, 50])
print("numpyarray.com - First element:", arr[0])
print("numpyarray.com - Last element:", arr[-1])
Output:

This example demonstrates how to access individual elements of a 1D array using positive and negative indices.
Slicing
Slicing allows you to extract a portion of an array:
import numpy as np
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
print("numpyarray.com - Slice from index 2 to 7:", arr[2:7])
print("numpyarray.com - Every other element:", arr[::2])
Output:

In this example, we extract a slice from index 2 to 7 (exclusive) and select every other element using step slicing.
Multi-dimensional Indexing
For multi-dimensional arrays, you can use comma-separated indices to access specific elements:
import numpy as np
arr_2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print("numpyarray.com - Element at row 1, column 2:", arr_2d[1, 2])
print("numpyarray.com - Second row:", arr_2d[1])
Output:

This example shows how to access individual elements and entire rows of a 2D array.
Boolean Indexing
Boolean indexing allows you to select elements based on conditions:
import numpy as np
arr = np.array([1, 2, 3, 4, 5])
mask = arr > 2
print("numpyarray.com - Elements greater than 2:", arr[mask])
Output:

In this example, we create a boolean mask to select elements greater than 2 from the array.
NumPy Array Operations and Mathematical Functions
NumPy provides a wide range of operations and mathematical functions that can be applied to arrays efficiently. Let’s explore some common operations:
Element-wise Operations
NumPy supports element-wise operations on arrays:
import numpy as np
arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
print("numpyarray.com - Addition:", arr1 + arr2)
print("numpyarray.com - Multiplication:", arr1 * arr2)
print("numpyarray.com - Exponentiation:", arr1 ** 2)
Output:

This example demonstrates element-wise addition, multiplication, and exponentiation of arrays.
Broadcasting
Broadcasting allows NumPy to perform operations on arrays with different shapes:
import numpy as np
arr = np.array([[1, 2, 3], [4, 5, 6]])
scalar = 10
print("numpyarray.com - Array + scalar:")
print(arr + scalar)
Output:

In this example, the scalar value is broadcast to match the shape of the array, allowing element-wise addition.
Universal Functions (ufuncs)
NumPy provides a set of universal functions that operate element-wise on arrays:
import numpy as np
arr = np.array([-1, 0, 1])
print("numpyarray.com - Absolute value:", np.abs(arr))
print("numpyarray.com - Exponential:", np.exp(arr))
print("numpyarray.com - Square root of absolute values:", np.sqrt(np.abs(arr)))
Output:

This example demonstrates the use of universal functions for calculating absolute values, exponentials, and square roots.
Array Reshaping and Manipulation
NumPy offers various methods to reshape and manipulate arrays. Let’s explore some common techniques:
Reshaping Arrays
The reshape() method allows you to change the shape of an array without changing its data:
import numpy as np
arr = np.arange(12)
reshaped_arr = arr.reshape((3, 4))
print("numpyarray.com - Reshaped array:")
print(reshaped_arr)
Output:
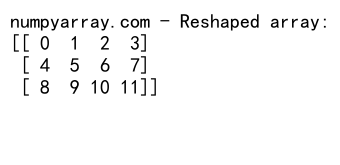
This example reshapes a 1D array with 12 elements into a 2D array with 3 rows and 4 columns.
Transposing Arrays
The transpose() method or T attribute can be used to transpose an array:
import numpy as np
arr = np.array([[1, 2, 3], [4, 5, 6]])
transposed_arr = arr.T
print("numpyarray.com - Transposed array:")
print(transposed_arr)
Output:

This example demonstrates how to transpose a 2D array, swapping its rows and columns.
Stacking Arrays
NumPy provides functions to stack arrays vertically or horizontally:
import numpy as np
arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
vertical_stack = np.vstack((arr1, arr2))
horizontal_stack = np.hstack((arr1, arr2))
print("numpyarray.com - Vertical stack:")
print(vertical_stack)
print("numpyarray.com - Horizontal stack:")
print(horizontal_stack)
Output:

This example shows how to stack two 1D arrays vertically and horizontally.
NumPy Array Aggregation and Statistics
NumPy provides various functions for computing statistics and aggregating data in arrays. Let’s explore some common operations:
Basic Statistics
NumPy offers functions to compute basic statistics on arrays:
import numpy as np
arr = np.array([1, 2, 3, 4, 5])
print("numpyarray.com - Mean:", np.mean(arr))
print("numpyarray.com - Median:", np.median(arr))
print("numpyarray.com - Standard deviation:", np.std(arr))
Output:

This example demonstrates how to calculate the mean, median, and standard deviation of an array.
Aggregation Along Axes
For multi-dimensional arrays, you can perform aggregations along specific axes:
import numpy as np
arr_2d = np.array([[1, 2, 3], [4, 5, 6]])
print("numpyarray.com - Sum along rows:", np.sum(arr_2d, axis=1))
print("numpyarray.com - Max along columns:", np.max(arr_2d, axis=0))
Output:

This example shows how to compute the sum along rows and the maximum along columns of a 2D array.
Cumulative Operations
NumPy provides functions for cumulative operations on arrays:
import numpy as np
arr = np.array([1, 2, 3, 4, 5])
print("numpyarray.com - Cumulative sum:", np.cumsum(arr))
print("numpyarray.com - Cumulative product:", np.cumprod(arr))
Output:

This example demonstrates how to compute the cumulative sum and cumulative product of an array.
Advanced Array Concepts
Let’s explore some advanced concepts and techniques for working with NumPy Array:
Structured Arrays
Structured arrays allow you to define complex data types with named fields:
import numpy as np
dt = np.dtype([('name', 'U10'), ('age', 'i4'), ('weight', 'f4')])
arr = np.array([('Alice', 25, 55.5), ('Bob', 30, 70.2)], dtype=dt)
print("numpyarray.com - Structured array:")
print(arr)
print("numpyarray.com - Ages:", arr['age'])
Output:

This example creates a structured array with fields for name, age, and weight, and demonstrates how to access individual fields.
Memory Views
Memory views provide a way to access array data without copying:
import numpy as np
arr = np.array([1, 2, 3, 4, 5])
mem_view = memoryview(arr)
print("numpyarray.com - Memory view:", mem_view)
print("numpyarray.com - First element via memory view:", mem_view[0])
Output:

This example creates a memory view of a NumPy array and demonstrates how to access elements through the view.
Masked Arrays
Masked arrays allow you to work with arrays that have missing or invalid data:
import numpy as np
arr = np.array([1, 2, -999, 4, 5])
masked_arr = np.ma.masked_array(arr, mask=[False, False, True, False, False])
print("numpyarray.com - Masked array:", masked_arr)
print("numpyarray.com - Mean of masked array:", np.ma.mean(masked_arr))
Output:

This example creates a masked array where the value -999 is treated as invalid, and demonstrates how to compute statistics on the masked array.
Performance Optimization with NumPy Array
NumPy Array are designed for high-performance numerical computing. Here are some tips for optimizing your code:
Vectorization
Vectorization is the process of replacing explicit loops with array operations:
import numpy as np
# Slow, explicit loop
def slow_sum_of_squares(n):
result = 0
for i in range(n):
result += i ** 2
return result
# Fast, vectorized version
def fast_sum_of_squares(n):
return np.sum(np.arange(n) ** 2)
n = 1000000
print("numpyarray.com - Sum of squares (slow):", slow_sum_of_squares(n))
print("numpyarray.com - Sum of squares (fast):", fast_sum_of_squares(n))
Output:

This example demonstrates how vectorization can significantly improve performance for large arrays.
Using Built-in Functions
NumPy’s built-in functions are optimized for performance:
import numpy as np
arr = np.random.rand(1000000)
# Slow, Python-level loop
def slow_mean(arr):
return sum(arr) / len(arr)
# Fast, using NumPy's built-in function
def fast_mean(arr):
return np.mean(arr)
print("numpyarray.com - Mean (slow):", slow_mean(arr))
print("numpyarray.com - Mean (fast):", fast_mean(arr))
Output:

This example shows how using NumPy’s built-in functions can be much faster than implementing operations manually.
NumPy Array Input and Output
NumPy provides various functions for reading and writing array data to files:
Saving and Loading Arrays
You can save and load NumPy Array using np.save() and np.load():
import numpy as np
arr = np.array([1, 2, 3, 4, 5])
# Save array to file
np.save('numpyarray_com_example.npy', arr)
# Load array from file
loaded_arr = np.load('numpyarray_com_example.npy')
print("numpyarray.com - Loaded array:", loaded_arr)
Output:

This example demonstrates how to save a NumPy array to a file and then load it back into memory.
Text File I/O
NumPy can read and write arrays to text files:
import numpy as np
arr = np.array([[1, 2, 3], [4, 5, 6]])
# Save array to text file
np.savetxt('numpyarray_com_example.txt', arr)
# Load array from text file
loaded_arr = np.loadtxt('numpyarray_com_example.txt')
print("numpyarray.com - Loaded array from text file:")
print(loaded_arr)
Output:

This example shows how to save a NumPy array to a text file and then read it back into memory.
Working with Large Datasets
NumPy Array are efficient for handling large datasets. Here are some techniques for working with big data:
Memory-mapped Arrays
Memory-mapped arrays allow you to work with large datasets that don’t fit in memory:
import numpy as np
# Create a large memory-mapped array
mm_arr = np.memmap('numpyarray_com_large_file.dat', dtype='float32', mode='w+', shape=(1000000, 10))
# Write data to the memory-mapped array
mm_arr[:] = np.random.random((1000000, 10))
# Access a portion of the array
print("numpyarray.com - First 5 rows of memory-mapped array:")
print(mm_arr[:5])
Output:

This example creates a large memory-mapped array and demonstrates how to write and read data from it.
Chunked Processing
For datasets too large to process at once, you can use chunked processing:
import numpy as np
# Simulate a large dataset
large_arr = np.random.rand(1000000, 10)
# Process the data in chunks
chunk_size = 100000
num_chunks = len(large_arr) // chunk_size
for i in range(num_chunks):
start = i * chunk_size
end = (i + 1) * chunk_size
chunk = large_arr[start:end]
# Process the chunk (e.g., compute mean)
chunk_mean = np.mean(chunk, axis=0)
print(f"numpyarray.com - Mean of chunk {i}:", chunk_mean)
Output:
This example demonstrates how to process a large array in smaller chunks to manage memory usage.
NumPy Array Broadcasting
Broadcasting is a powerful feature of NumPy that allows operations between arrays of different shapes. Let’s explore this concept in more detail:
Rules of Broadcasting
Broadcasting follows these rules: 1. Arrays with fewer dimensions are padded with ones on the left.
2. Arrays with too few elements in a dimension are repeated to match the other array.
import numpy as np
# Broadcasting scalar to array
arr = np.array([1, 2, 3, 4])
result = arr * 2
print("numpyarray.com - Broadcasting scalar:", result)
# Broadcasting 1D array to 2D array
arr_2d = np.array([[1, 2, 3], [4, 5, 6]])
arr_1d = np.array([10, 20, 30])
result = arr_2d + arr_1d
print("numpyarray.com - Broadcasting 1D to 2D:")
print(result)
Output:

This example demonstrates broadcasting a scalar to an array and a 1D array to a 2D array.
Advanced Broadcasting
Broadcasting can be used with more complex array shapes:
import numpy as np
# Broadcasting with 3D and 2D arrays
arr_3d = np.ones((3, 4, 5))
arr_2d = np.arange(20).reshape(4, 5)
result = arr_3d + arr_2d
print("numpyarray.com - Broadcasting 3D and 2D arrays:")
print(result.shape)
Output:

This example shows how broadcasting works with 3D and 2D arrays.
NumPy Array Sorting and Searching
NumPy provides efficient algorithms for sorting and searching arrays:
Sorting Arrays
You can sort NumPy Array using the sort() function:
import numpy as np
arr = np.array([3, 1, 4, 1, 5, 9, 2, 6])
sorted_arr = np.sort(arr)
print("numpyarray.com - Sorted array:", sorted_arr)
# Sort 2D array along columns
arr_2d = np.array([[3, 1, 4], [1, 5, 9], [2, 6, 5]])
sorted_2d = np.sort(arr_2d, axis=0)
print("numpyarray.com - Sorted 2D array along columns:")
print(sorted_2d)
Output:

This example demonstrates sorting 1D and 2D arrays.
Searching Arrays
NumPy offers functions for searching arrays:
import numpy as np
arr = np.array([1, 2, 3, 4, 5])
# Find indices where elements are greater than 3
indices = np.where(arr > 3)
print("numpyarray.com - Indices where elements > 3:", indices[0])
# Find the index of the maximum element
max_index = np.argmax(arr)
print("numpyarray.com - Index of maximum element:", max_index)
Output:

This example shows how to search for elements in an array based on conditions and find the index of the maximum element.
NumPy Array Set Operations
NumPy provides functions for performing set operations on arrays:
Unique Elements
You can find unique elements in an array using np.unique():
import numpy as np
arr = np.array([1, 2, 2, 3, 3, 3, 4, 5, 5])
unique_elements = np.unique(arr)
print("numpyarray.com - Unique elements:", unique_elements)
Output:

This example demonstrates how to find unique elements in an array.
Set Operations
NumPy offers functions for set operations like union and intersection:
import numpy as np
arr1 = np.array([1, 2, 3, 4, 5])
arr2 = np.array([4, 5, 6, 7, 8])
# Union of two arrays
union = np.union1d(arr1, arr2)
print("numpyarray.com - Union:", union)
# Intersection of two arrays
intersection = np.intersect1d(arr1, arr2)
print("numpyarray.com - Intersection:", intersection)
Output:

This example shows how to perform union and intersection operations on NumPy Array.
NumPy array Conclusion
NumPy array are a powerful and versatile tool for numerical computing in Python. They provide efficient storage and operations for large datasets, making them essential for scientific computing, data analysis, and machine learning. By mastering NumPy Array, you can significantly improve the performance and readability of your numerical Python code.
In this comprehensive guide, we’ve covered a wide range of topics related to NumPy Array, including:
- Creating and manipulating arrays
- Array indexing and slicing
- Array operations and mathematical functions
- Reshaping and manipulating array dimensions
- Statistical operations and aggregations
- Advanced array concepts like structured arrays and masked arrays
- Performance optimization techniques
- Input/output operations for arrays
- Working with large datasets
- Broadcasting
- Sorting and searching arrays
- Set operations on arrays
By applying these concepts and techniques, you can leverage the full power of NumPy Array in your projects. Remember to experiment with different approaches and always consider the specific requirements of your data and computations when working with NumPy Array.
As you continue to work with NumPy, you’ll discover even more advanced features and optimizations that can further enhance your data processing capabilities. The NumPy documentation is an excellent resource for exploring additional functionality and staying up-to-date with the latest developments in the library.
With its combination of performance, flexibility, and ease of use, NumPy remains a cornerstone of the scientific Python ecosystem. Whether you’re working on small-scale data analysis or large-scale machine learning projects, mastering NumPy Array will undoubtedly improve your ability to work with numerical data efficiently and effectively.