Generative Adversarial Nets

We propose a new framework for estimating generative models via an adversarial process, in which we simultaneously train two models: a generative model G𝐺G that captures the data distribution, and a discriminative model D𝐷D that estimates the probability that a sample came from the training data rather than G𝐺G. The training procedure for G𝐺G is to maximize the probability of D𝐷D making a mistake. This framework corresponds to a minimax two-player game. In the space of arbitrary functions G𝐺G and D𝐷D, a unique solution exists, with G𝐺G recovering the training data distribution and D𝐷D equal to 1212\frac{1}{2} everywhere. In the case where G𝐺G and D𝐷D are defined by multilayer perceptrons, the entire system can be trained with backpropagation. There is no need for any Markov chains or unrolled approximate inference networks during either training or generation of samples. Experiments demonstrate the potential of the framework through qualitative and quantitative evaluation of the generated samples.

The promise of deep learning is to discover rich, hierarchical models [2] that represent probability distributions over the kinds of data encountered in artificial intelligence applications, such as natural images, audio waveforms containing speech, and symbols in natural language corpora. So far, the most striking successes in deep learning have involved discriminative models, usually those that map a high-dimensional, rich sensory input to a class label [14, 22]. These striking successes have primarily been based on the backpropagation and dropout algorithms, using piecewise linear units  [19, 9, 10] which have a particularly well-behaved gradient . Deep generative models have had less of an impact, due to the difficulty of approximating many intractable probabilistic computations that arise in maximum likelihood estimation and related strategies, and due to difficulty of leveraging the benefits of piecewise linear units in the generative context. We propose a new generative model estimation procedure that sidesteps these difficulties.

In the proposed adversarial nets framework, the generative model is pitted against an adversary: a discriminative model that learns to determine whether a sample is from the model distribution or the data distribution. The generative model can be thought of as analogous to a team of counterfeiters, trying to produce fake currency and use it without detection, while the discriminative model is analogous to the police, trying to detect the counterfeit currency. Competition in this game drives both teams to improve their methods until the counterfeits are indistiguishable from the genuine articles.

This framework can yield specific training algorithms for many kinds of model and optimization algorithm. In this article, we explore the special case when the generative model generates samples by passing random noise through a multilayer perceptron, and the discriminative model is also a multilayer perceptron. We refer to this special case as adversarial nets. In this case, we can train both models using only the highly successful backpropagation and dropout algorithms [17] and sample from the generative model using only forward propagation. No approximate inference or Markov chains are necessary.

An alternative to directed graphical models with latent variables are undirected graphical models with latent variables, such as restricted Boltzmann machines (RBMs) [27, 16], deep Boltzmann machines (DBMs) [26] and their numerous variants. The interactions within such models are represented as the product of unnormalized potential functions, normalized by a global summation/integration over all states of the random variables. This quantity (the partition function) and its gradient are intractable for all but the most trivial instances, although they can be estimated by Markov chain Monte Carlo (MCMC) methods. Mixing poses a significant problem for learning algorithms that rely on MCMC [3, 5].

Deep belief networks (DBNs) [16] are hybrid models containing a single undirected layer and several directed layers. While a fast approximate layer-wise training criterion exists, DBNs incur the computational difficulties associated with both undirected and directed models.

Alternative criteria that do not approximate or bound the log-likelihood have also been proposed, such as score matching [18] and noise-contrastive estimation (NCE) [13]. Both of these require the learned probability density to be analytically specified up to a normalization constant. Note that in many interesting generative models with several layers of latent variables (such as DBNs and DBMs), it is not even possible to derive a tractable unnormalized probability density. Some models such as denoising auto-encoders [30] and contractive autoencoders have learning rules very similar to score matching applied to RBMs. In NCE, as in this work, a discriminative training criterion is employed to fit a generative model. However, rather than fitting a separate discriminative model, the generative model itself is used to discriminate generated data from samples a fixed noise distribution. Because NCE uses a fixed noise distribution, learning slows dramatically after the model has learned even an approximately correct distribution over a small subset of the observed variables.

Finally, some techniques do not involve defining a probability distribution explicitly, but rather train a generative machine to draw samples from the desired distribution. This approach has the advantage that such machines can be designed to be trained by back-propagation. Prominent recent work in this area includes the generative stochastic network (GSN) framework [5], which extends generalized denoising auto-encoders [4]: both can be seen as defining a parameterized Markov chain, i.e., one learns the parameters of a machine that performs one step of a generative Markov chain. Compared to GSNs, the adversarial nets framework does not require a Markov chain for sampling. Because adversarial nets do not require feedback loops during generation, they are better able to leverage piecewise linear units [19, 9, 10], which improve the performance of backpropagation but have problems with unbounded activation when used ina feedback loop. More recent examples of training a generative machine by back-propagating into it include recent work on auto-encoding variational Bayes [20] and stochastic backpropagation [24].

The adversarial modeling framework is most straightforward to apply when the models are both multilayer perceptrons. To learn the generator’s distribution pgsubscript𝑝𝑔p_{g} over data 𝒙𝒙\bm{x}, we define a prior on input noise variables p𝒛​(𝒛)subscript𝑝𝒛𝒛p_{\bm{z}}(\bm{z}), then represent a mapping to data space as G​(𝒛;θg)𝐺𝒛subscript𝜃𝑔G(\bm{z};\theta_{g}), where G𝐺G is a differentiable function represented by a multilayer perceptron with parameters θgsubscript𝜃𝑔\theta_{g}. We also define a second multilayer perceptron D​(𝒙;θd)𝐷𝒙subscript𝜃𝑑D(\bm{x};\theta_{d}) that outputs a single scalar. D​(𝒙)𝐷𝒙D(\bm{x}) represents the probability that 𝒙𝒙\bm{x} came from the data rather than pgsubscript𝑝𝑔p_{g}. We train D𝐷D to maximize the probability of assigning the correct label to both training examples and samples from G𝐺G. We simultaneously train G𝐺G to minimize log⁡(1−D​(G​(𝒛)))1𝐷𝐺𝒛\log(1-D(G(\bm{z}))):

In other words, D𝐷D and G𝐺G play the following two-player minimax game with value function V​(G,D)𝑉𝐺𝐷V(G,D):

minG⁡maxD⁡V​(D,G)=𝔼𝒙∼pdata​(𝒙)​[log⁡D​(𝒙)]+𝔼𝒛∼p𝒛​(𝒛)​[log⁡(1−D​(G​(𝒛)))].subscript𝐺subscript𝐷𝑉𝐷𝐺subscript𝔼similar-to𝒙subscript𝑝data𝒙delimited-[]𝐷𝒙subscript𝔼similar-to𝒛subscript𝑝𝒛𝒛delimited-[]1𝐷𝐺𝒛\min_{G}\max_{D}V(D,G)=\mathbb{E}_{\bm{x}\sim p_{\text{data}}(\bm{x})}[\log D(\bm{x})]+\mathbb{E}_{\bm{z}\sim p_{\bm{z}}(\bm{z})}[\log(1-D(G(\bm{z})))].

(1)

In the next section, we present a theoretical analysis of adversarial nets, essentially showing that the training criterion allows one to recover the data generating distribution as G𝐺G and D𝐷D are given enough capacity, i.e., in the non-parametric limit. See Figure 1 for a less formal, more pedagogical explanation of the approach. In practice, we must implement the game using an iterative, numerical approach. Optimizing D𝐷D to completion in the inner loop of training is computationally prohibitive, and on finite datasets would result in overfitting. Instead, we alternate between k𝑘k steps of optimizing D𝐷D and one step of optimizing G𝐺G. This results in D𝐷D being maintained near its optimal solution, so long as G𝐺G changes slowly enough. This strategy is analogous to the way that SML/PCD [31, 29] training maintains samples from a Markov chain from one learning step to the next in order to avoid burning in a Markov chain as part of the inner loop of learning. The procedure is formally presented in Algorithm 1.

In practice, equation 1 may not provide sufficient gradient for G𝐺G to learn well. Early in learning, when G𝐺G is poor, D𝐷D can reject samples with high confidence because they are clearly different from the training data. In this case, log⁡(1−D​(G​(𝒛)))1𝐷𝐺𝒛\log(1-D(G(\bm{z}))) saturates. Rather than training G𝐺G to minimize log⁡(1−D​(G​(𝒛)))1𝐷𝐺𝒛\log(1-D(G(\bm{z}))) we can train G𝐺G to maximize log⁡D​(G​(𝒛))𝐷𝐺𝒛\log D(G(\bm{z})). This objective function results in the same fixed point of the dynamics of G𝐺G and D𝐷D but provides much stronger gradients early in learning.

…

(a)

(b)

(c)

(d)

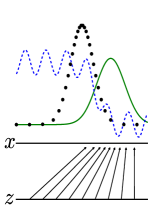
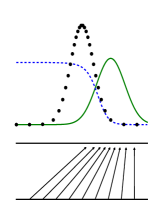
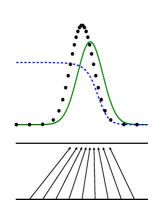
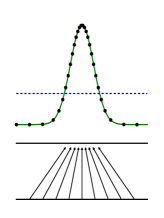
Figure 1: Generative adversarial nets are trained by simultaneously updating the discriminative distribution (D𝐷D, blue, dashed line) so that it discriminates between samples from the data generating distribution (black, dotted line) p𝒙subscript𝑝𝒙p_{\bm{x}} from those of the generative distribution pgsubscript𝑝𝑔p_{g} (G) (green, solid line). The lower horizontal line is the domain from which 𝒛𝒛\bm{z} is sampled, in this case uniformly. The horizontal line above is part of the domain of 𝒙𝒙\bm{x}. The upward arrows show how the mapping 𝒙=G​(𝒛)𝒙𝐺𝒛\bm{x}=G(\bm{z}) imposes the non-uniform distribution pgsubscript𝑝𝑔p_{g} on transformed samples. G𝐺G contracts in regions of high density and expands in regions of low density of pgsubscript𝑝𝑔p_{g}. (a) Consider an adversarial pair near convergence: pgsubscript𝑝𝑔p_{g} is similar to pdatasubscript𝑝datap_{\text{data}} and D𝐷D is a partially accurate classifier. (b) In the inner loop of the algorithm D𝐷D is trained to discriminate samples from data, converging to D∗​(𝒙)=pdata​(𝒙)pdata​(𝒙)+pg​(𝒙)superscript𝐷𝒙subscript𝑝data𝒙subscript𝑝data𝒙subscript𝑝𝑔𝒙D^{*}(\bm{x})=\frac{p_{\text{data}}(\bm{x})}{p_{\text{data}}(\bm{x})+p_{g}(\bm{x})}. (c) After an update to G𝐺G, gradient of D𝐷D has guided G​(𝒛)𝐺𝒛G(\bm{z}) to flow to regions that are more likely to be classified as data. (d) After several steps of training, if G𝐺G and D𝐷D have enough capacity, they will reach a point at which both cannot improve because pg=pdatasubscript𝑝𝑔subscript𝑝datap_{g}=p_{\text{data}}. The discriminator is unable to differentiate between the two distributions, i.e. D​(𝒙)=12𝐷𝒙12D(\bm{x})=\frac{1}{2}.

Algorithm 1 Minibatch stochastic gradient descent training of generative adversarial nets. The number of steps to apply to the discriminator, k𝑘k, is a hyperparameter. We used k=1𝑘1k=1, the least expensive option, in our experiments.

  for number of training iterations do

        ∙∙\bullet Sample minibatch of m𝑚m noise samples {𝒛(1),…,𝒛(m)}superscript𝒛1…superscript𝒛𝑚\{\bm{z}^{(1)},\dots,\bm{z}^{(m)}\} from noise prior pg​(𝒛)subscript𝑝𝑔𝒛p_{g}(\bm{z}).

        ∙∙\bullet Sample minibatch of m𝑚m examples {𝒙(1),…,𝒙(m)}superscript𝒙1…superscript𝒙𝑚\{\bm{x}^{(1)},\dots,\bm{x}^{(m)}\} from data generating distribution pdata​(𝒙)subscript𝑝data𝒙p_{\text{data}}(\bm{x}).

        ∙∙\bullet Update the discriminator by ascending its stochastic gradient:

∇θd1m​∑i=1m[log⁡D​(𝒙(i))+log⁡(1−D​(G​(𝒛(i))))].subscript∇subscript𝜃𝑑1𝑚superscriptsubscript𝑖1𝑚delimited-[]𝐷superscript𝒙𝑖1𝐷𝐺superscript𝒛𝑖\nabla_{\theta_{d}}\frac{1}{m}\sum_{i=1}^{m}\left[\log D\left(\bm{x}^{(i)}\right)+\log\left(1-D\left(G\left(\bm{z}^{(i)}\right)\right)\right)\right].

     ∙∙\bullet Sample minibatch of m𝑚m noise samples {𝒛(1),…,𝒛(m)}superscript𝒛1…superscript𝒛𝑚\{\bm{z}^{(1)},\dots,\bm{z}^{(m)}\} from noise prior pg​(𝒛)subscript𝑝𝑔𝒛p_{g}(\bm{z}).

     ∙∙\bullet Update the generator by descending its stochastic gradient:

∇θg1m​∑i=1mlog⁡(1−D​(G​(𝒛(i)))).subscript∇subscript𝜃𝑔1𝑚superscriptsubscript𝑖1𝑚1𝐷𝐺superscript𝒛𝑖\nabla_{\theta_{g}}\frac{1}{m}\sum_{i=1}^{m}\log\left(1-D\left(G\left(\bm{z}^{(i)}\right)\right)\right).

  end forThe gradient-based updates can use any standard gradient-based learning rule. We used momentum in our experiments.

The generator G𝐺G implicitly defines a probability distribution pgsubscript𝑝𝑔p_{g} as the distribution of the samples G​(𝒛)𝐺𝒛G(\bm{z}) obtained when 𝒛∼p𝒛similar-to𝒛subscript𝑝𝒛\bm{z}\sim p_{\bm{z}}. Therefore, we would like Algorithm 1 to converge to a good estimator of pdatasubscript𝑝datap_{\text{data}}, if given enough capacity and training time. The results of this section are done in a non-parametric setting, e.g. we represent a model with infinite capacity by studying convergence in the space of probability density functions.

We will show in section 4.1 that this minimax game has a global optimum for pg=pdatasubscript𝑝𝑔subscript𝑝datap_{g}=p_{\text{data}}. We will then show in section 4.2 that Algorithm 1 optimizes Eq 1, thus obtaining the desired result.

We first consider the optimal discriminator D𝐷D for any given generator G𝐺G.

For G𝐺G fixed, the optimal discriminator D𝐷D is

DG∗​(𝒙)=pdata​(𝒙)pdata​(𝒙)+pg​(𝒙)subscriptsuperscript𝐷𝐺𝒙subscript𝑝data𝒙subscript𝑝data𝒙subscript𝑝𝑔𝒙D^{*}_{G}(\bm{x})=\frac{p_{\text{data}}(\bm{x})}{p_{\text{data}}(\bm{x})+p_{g}(\bm{x})}

(2)

The training criterion for the discriminator D, given any generator G𝐺G, is to maximize the quantity V​(G,D)𝑉𝐺𝐷V(G,D)

V​(G,D)=𝑉𝐺𝐷absent\displaystyle V(G,D)=

∫𝒙pdata​(𝒙)​log⁡(D​(𝒙))​𝑑x+∫zp𝒛​(𝒛)​log⁡(1−D​(g​(𝒛)))​𝑑zsubscript𝒙subscript𝑝data𝒙𝐷𝒙differential-d𝑥subscript𝑧subscript𝑝𝒛𝒛1𝐷𝑔𝒛differential-d𝑧\displaystyle\int_{\bm{x}}p_{\text{data}}(\bm{x})\log(D(\bm{x}))dx+\int_{z}p_{\bm{z}}(\bm{z})\log(1-D(g(\bm{z})))dz

=\displaystyle=

∫𝒙pdata​(𝒙)​log⁡(D​(𝒙))+pg​(𝒙)​log⁡(1−D​(𝒙))​d​xsubscript𝒙subscript𝑝data𝒙𝐷𝒙subscript𝑝𝑔𝒙1𝐷𝒙𝑑𝑥\displaystyle\int_{\bm{x}}p_{\text{data}}(\bm{x})\log(D(\bm{x}))+p_{g}(\bm{x})\log(1-D(\bm{x}))dx

(3)

For any (a,b)∈ℝ2∖{0,0}𝑎𝑏superscriptℝ200(a,b)\in\mathbb{R}^{2}\setminus\{0,0\}, the function y→a​log⁡(y)+b​log⁡(1−y)→𝑦𝑎𝑦𝑏1𝑦y\rightarrow a\log(y)+b\log(1-y) achieves its maximum in [0,1]01[0,1] at aa+b𝑎𝑎𝑏\frac{a}{a+b}. The discriminator does not need to be defined outside of S​u​p​p​(pdata)∪S​u​p​p​(pg)𝑆𝑢𝑝𝑝subscript𝑝data𝑆𝑢𝑝𝑝subscript𝑝𝑔Supp(p_{\text{data}})\cup Supp(p_{g}), concluding the proof. ∎

Note that the training objective for D𝐷D can be interpreted as maximizing the log-likelihood for estimating the conditional probability P​(Y=y|𝒙)𝑃𝑌conditional𝑦𝒙P(Y=y|\bm{x}), where Y𝑌Y indicates whether 𝒙𝒙\bm{x} comes from pdatasubscript𝑝datap_{\text{data}} (with y=1𝑦1y=1) or from pgsubscript𝑝𝑔p_{g} (with y=0𝑦0y=0). The minimax game in Eq. 1 can now be reformulated as:

C​(G)=𝐶𝐺absent\displaystyle C(G)=

maxD⁡V​(G,D)subscript𝐷𝑉𝐺𝐷\displaystyle\max_{D}V(G,D)

=\displaystyle=

𝔼𝒙∼pdata​[log⁡DG∗​(𝒙)]+𝔼𝒛∼p𝒛​[log⁡(1−DG∗​(G​(𝒛)))]subscript𝔼similar-to𝒙subscript𝑝datadelimited-[]subscriptsuperscript𝐷𝐺𝒙subscript𝔼similar-to𝒛subscript𝑝𝒛delimited-[]1subscriptsuperscript𝐷𝐺𝐺𝒛\displaystyle\mathbb{E}_{\bm{x}\sim p_{\text{data}}}[\log D^{*}_{G}(\bm{x})]+\mathbb{E}_{\bm{z}\sim p_{\bm{z}}}[\log(1-D^{*}_{G}(G(\bm{z})))]

(4)

=\displaystyle=

𝔼𝒙∼pdata​[log⁡DG∗​(𝒙)]+𝔼𝒙∼pg​[log⁡(1−DG∗​(𝒙))]subscript𝔼similar-to𝒙subscript𝑝datadelimited-[]subscriptsuperscript𝐷𝐺𝒙subscript𝔼similar-to𝒙subscript𝑝𝑔delimited-[]1subscriptsuperscript𝐷𝐺𝒙\displaystyle\mathbb{E}_{\bm{x}\sim p_{\text{data}}}[\log D^{*}_{G}(\bm{x})]+\mathbb{E}_{\bm{x}\sim p_{g}}[\log(1-D^{*}_{G}(\bm{x}))]

=\displaystyle=

𝔼𝒙∼pdata​[log⁡pdata​(𝒙)Pdata​(𝒙)+pg​(𝒙)]+𝔼𝒙∼pg​[log⁡pg​(𝒙)pdata​(𝒙)+pg​(𝒙)]subscript𝔼similar-to𝒙subscript𝑝datadelimited-[]subscript𝑝data𝒙subscript𝑃data𝒙subscript𝑝𝑔𝒙subscript𝔼similar-to𝒙subscript𝑝𝑔delimited-[]subscript𝑝𝑔𝒙subscript𝑝data𝒙subscript𝑝𝑔𝒙\displaystyle\mathbb{E}_{\bm{x}\sim p_{\text{data}}}\left[\log\frac{p_{\text{data}}(\bm{x})}{P_{\text{data}}(\bm{x})+p_{g}(\bm{x})}\right]+\mathbb{E}_{\bm{x}\sim p_{g}}\left[\log\frac{p_{g}(\bm{x})}{p_{\text{data}}(\bm{x})+p_{g}(\bm{x})}\right]

The global minimum of the virtual training criterion C​(G)𝐶𝐺C(G) is achieved if and only if pg=pdatasubscript𝑝𝑔subscript𝑝datap_{g}=p_{\text{data}}. At that point, C​(G)𝐶𝐺C(G) achieves the value −log⁡44-\log 4.

For pg=pdatasubscript𝑝𝑔subscript𝑝datap_{g}=p_{\text{data}}, DG∗​(𝒙)=12subscriptsuperscript𝐷𝐺𝒙12D^{*}_{G}(\bm{x})=\frac{1}{2}, (consider Eq. 2). Hence, by inspecting Eq. 4.1 at DG∗​(𝒙)=12subscriptsuperscript𝐷𝐺𝒙12D^{*}_{G}(\bm{x})=\frac{1}{2}, we find C​(G)=log⁡12+log⁡12=−log⁡4𝐶𝐺12124C(G)=\log\frac{1}{2}+\log\frac{1}{2}=-\log 4. To see that this is the best possible value of C​(G)𝐶𝐺C(G), reached only for pg=pdatasubscript𝑝𝑔subscript𝑝datap_{g}=p_{\text{data}}, observe that

𝔼𝒙∼pdata​[−log⁡2]+𝔼𝒙∼pg​[−log⁡2]=−log⁡4subscript𝔼similar-to𝒙subscript𝑝datadelimited-[]2subscript𝔼similar-to𝒙subscript𝑝𝑔delimited-[]24\mathbb{E}_{\bm{x}\sim p_{\text{data}}}\left[-\log 2\right]+\mathbb{E}_{\bm{x}\sim p_{g}}\left[-\log 2\right]=-\log 4

and that by subtracting this expression from C​(G)=V​(DG∗,G)𝐶𝐺𝑉superscriptsubscript𝐷𝐺𝐺C(G)=V(D_{G}^{*},G), we obtain:

C​(G)=−log⁡(4)+K​L​(pdata∥pdata+pg2)+K​L​(pg∥pdata+pg2)𝐶𝐺4𝐾𝐿conditionalsubscript𝑝datasubscript𝑝datasubscript𝑝𝑔2𝐾𝐿conditionalsubscript𝑝𝑔subscript𝑝datasubscript𝑝𝑔2C(G)=-\log(4)+KL\left(p_{\text{data}}\left\|\frac{p_{\text{data}}+p_{g}}{2}\right.\right)+KL\left(p_{g}\left\|\frac{p_{\text{data}}+p_{g}}{2}\right.\right)

(5)

where KL is the Kullback–Leibler divergence. We recognize in the previous expression the Jensen–Shannon divergence between the model’s distribution and the data generating process:

C​(G)=−log⁡(4)+2⋅J​S​D​(pdata∥pg)𝐶𝐺4⋅2𝐽𝑆𝐷conditionalsubscript𝑝datasubscript𝑝𝑔C(G)=-\log(4)+2\cdot JSD\left(p_{\text{data}}\left\|p_{g}\right.\right)

(6)

Since the Jensen–Shannon divergence between two distributions is always non-negative and zero only when they are equal, we have shown that C∗=−log⁡(4)superscript𝐶4C^{*}=-\log(4) is the global minimum of C​(G)𝐶𝐺C(G) and that the only solution is pg=pdatasubscript𝑝𝑔subscript𝑝datap_{g}=p_{\text{data}}, i.e., the generative model perfectly replicating the data generating process. ∎

If G𝐺G and D𝐷D have enough capacity, and at each step of Algorithm 1, the discriminator is allowed to reach its optimum given G𝐺G, and pgsubscript𝑝𝑔p_{g} is updated so as to improve the criterion

𝔼𝒙∼pdata​[log⁡DG∗​(𝒙)]+𝔼𝒙∼pg​[log⁡(1−DG∗​(𝒙))]subscript𝔼similar-to𝒙subscript𝑝datadelimited-[]subscriptsuperscript𝐷𝐺𝒙subscript𝔼similar-to𝒙subscript𝑝𝑔delimited-[]1subscriptsuperscript𝐷𝐺𝒙\mathbb{E}_{\bm{x}\sim p_{\text{data}}}[\log D^{*}_{G}(\bm{x})]+\mathbb{E}_{\bm{x}\sim p_{g}}[\log(1-D^{*}_{G}(\bm{x}))]

then pgsubscript𝑝𝑔p_{g} converges to pdatasubscript𝑝datap_{\text{data}}

Consider V​(G,D)=U​(pg,D)𝑉𝐺𝐷𝑈subscript𝑝𝑔𝐷V(G,D)=U(p_{g},D) as a function of pgsubscript𝑝𝑔p_{g} as done in the above criterion. Note that U​(pg,D)𝑈subscript𝑝𝑔𝐷U(p_{g},D) is convex in pgsubscript𝑝𝑔p_{g}. The subderivatives of a supremum of convex functions include the derivative of the function at the point where the maximum is attained. In other words, if f​(x)=supα∈𝒜fα​(x)𝑓𝑥subscriptsupremum𝛼𝒜subscript𝑓𝛼𝑥f(x)=\sup_{\alpha\in\cal{A}}f_{\alpha}(x) and fα​(x)subscript𝑓𝛼𝑥f_{\alpha}(x) is convex in x𝑥x for every α𝛼\alpha, then ∂fβ​(x)∈∂fsubscript𝑓𝛽𝑥𝑓\partial f_{\beta}(x)\in\partial f if β=arg​supα∈𝒜fα​(x)𝛽subscriptsupremum𝛼𝒜subscript𝑓𝛼𝑥\beta=\arg\sup_{\alpha\in\cal{A}}f_{\alpha}(x). This is equivalent to computing a gradient descent update for pgsubscript𝑝𝑔p_{g} at the optimal D𝐷D given the corresponding G𝐺G. supDU​(pg,D)subscriptsupremum𝐷𝑈subscript𝑝𝑔𝐷\sup_{D}U(p_{g},D) is convex in pgsubscript𝑝𝑔p_{g} with a unique global optima as proven in Thm 1, therefore with sufficiently small updates of pgsubscript𝑝𝑔p_{g}, pgsubscript𝑝𝑔p_{g} converges to pxsubscript𝑝𝑥p_{x}, concluding the proof. ∎

In practice, adversarial nets represent a limited family of pgsubscript𝑝𝑔p_{g} distributions via the function G​(𝒛;θg)𝐺𝒛subscript𝜃𝑔G(\bm{z};\theta_{g}), and we optimize θgsubscript𝜃𝑔\theta_{g} rather than pgsubscript𝑝𝑔p_{g} itself. Using a multilayer perceptron to define G𝐺G introduces multiple critical points in parameter space. However, the excellent performance of multilayer perceptrons in practice suggests that they are a reasonable model to use despite their lack of theoretical guarantees.

We trained adversarial nets an a range of datasets including MNIST[23], the Toronto Face Database (TFD) [28], and CIFAR-10 [21]. The generator nets used a mixture of rectifier linear activations [19, 9] and sigmoid activations, while the discriminator net used maxout [10] activations. Dropout [17] was applied in training the discriminator net. While our theoretical framework permits the use of dropout and other noise at intermediate layers of the generator, we used noise as the input to only the bottommost layer of the generator network.

We estimate probability of the test set data under pgsubscript𝑝𝑔p_{g} by fitting a Gaussian Parzen window to the samples generated with G𝐺G and reporting the log-likelihood under this distribution. The σ𝜎\sigma parameter of the Gaussians was obtained by cross validation on the validation set. This procedure was introduced in Breuleux et al. [8] and used for various generative models for which the exact likelihood is not tractable [25, 3, 5]. Results are reported in Table 1. This method of estimating the likelihood has somewhat high variance and does not perform well in high dimensional spaces but it is the best method available to our knowledge. Advances in generative models that can sample but not estimate likelihood directly motivate further research into how to evaluate such models.

Table 1: Parzen window-based log-likelihood estimates. The reported numbers on MNIST are the mean log-likelihood of samples on test set, with the standard error of the mean computed across examples. On TFD, we computed the standard error across folds of the dataset, with a different σ𝜎\sigma chosen using the validation set of each fold. On TFD, σ𝜎\sigma was cross validated on each fold and mean log-likelihood on each fold were computed. For MNIST we compare against other models of the real-valued (rather than binary) version of dataset.

In Figures 2 and 3 we show samples drawn from the generator net after training. While we make no claim that these samples are better than samples generated by existing methods, we believe that these samples are at least competitive with the better generative models in the literature and highlight the potential of the adversarial framework.

a)

b)

c)

d)

Figure 2: Visualization of samples from the model. Rightmost column shows the nearest training example of the neighboring sample, in order to demonstrate that the model has not memorized the training set. Samples are fair random draws, not cherry-picked. Unlike most other visualizations of deep generative models, these images show actual samples from the model distributions, not conditional means given samples of hidden units. Moreover, these samples are uncorrelated because the sampling process does not depend on Markov chain mixing. a) MNIST b) TFD c) CIFAR-10 (fully connected model) d) CIFAR-10 (convolutional discriminator and “deconvolutional” generator)

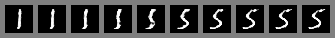
Figure 3: Digits obtained by linearly interpolating between coordinates in 𝒛𝒛\bm{z} space of the full model.

Table 2: Challenges in generative modeling: a summary of the difficulties encountered by different approaches to deep generative modeling for each of the major operations involving a model.

This new framework comes with advantages and disadvantages relative to previous modeling frameworks. The disadvantages are primarily that there is no explicit representation of pg​(𝒙)subscript𝑝𝑔𝒙p_{g}(\bm{x}), and that D𝐷D must be synchronized well with G𝐺G during training (in particular, G𝐺G must not be trained too much without updating D𝐷D, in order to avoid “the Helvetica scenario” in which G𝐺G collapses too many values of 𝐳𝐳\mathbf{z} to the same value of 𝐱𝐱\mathbf{x} to have enough diversity to model pdatasubscript𝑝datap_{\text{data}}), much as the negative chains of a Boltzmann machine must be kept up to date between learning steps. The advantages are that Markov chains are never needed, only backprop is used to obtain gradients, no inference is needed during learning, and a wide variety of functions can be incorporated into the model. Table 2 summarizes the comparison of generative adversarial nets with other generative modeling approaches.

The aforementioned advantages are primarily computational. Adversarial models may also gain some statistical advantage from the generator network not being updated directly with data examples, but only with gradients flowing through the discriminator. This means that components of the input are not copied directly into the generator’s parameters. Another advantage of adversarial networks is that they can represent very sharp, even degenerate distributions, while methods based on Markov chains require that the distribution be somewhat blurry in order for the chains to be able to mix between modes.

This framework admits many straightforward extensions:

A conditional generative model p​(𝒙∣𝒄)𝑝conditional𝒙𝒄p(\\bm{x}\\mid\\bm{c}) can be obtained by adding 𝒄𝒄\\bm{c} as input to both G𝐺G and D𝐷D.

Learned approximate inference can be performed by training an auxiliary network to predict 𝒛𝒛\\bm{z} given 𝒙𝒙\\bm{x}. This is similar to the inference net trained by the wake-sleep algorithm  \[[15](#bib.bib15)\] but with the advantage that the inference net may be trained for a fixed generator net after the generator net has finished training.

One can approximately model all conditionals p​(𝒙S∣𝒙S̸)𝑝conditionalsubscript𝒙𝑆subscript𝒙italic-S̸p(\\bm{x}\_{S}\\mid\\bm{x}\_{\\not S}) where S𝑆S is a subset of the indices of 𝒙𝒙\\bm{x} by training a family of conditional models that share parameters. Essentially, one can use adversarial nets to implement a stochastic extension of the deterministic MP-DBM \[[11](#bib.bib11)\].

Semi-supervised learning: features from the discriminator or inference net could improve performance of classifiers when limited labeled data is available.

Efficiency improvements: training could be accelerated greatly by divising better methods for coordinating G𝐺G and D𝐷D or determining better distributions to sample 𝐳𝐳\\mathbf{z} from during training.

This paper has demonstrated the viability of the adversarial modeling framework, suggesting that these research directions could prove useful.

We would like to acknowledge Patrice Marcotte, Olivier Delalleau, Kyunghyun Cho, Guillaume Alain and Jason Yosinski for helpful discussions. Yann Dauphin shared his Parzen window evaluation code with us. We would like to thank the developers of Pylearn2 [12] and Theano [7, 1], particularly Frédéric Bastien who rushed a Theano feature specifically to benefit this project. Arnaud Bergeron provided much-needed support with LaTeX typesetting. We would also like to thank CIFAR, and Canada Research Chairs for funding, and Compute Canada, and Calcul Québec for providing computational resources. Ian Goodfellow is supported by the 2013 Google Fellowship in Deep Learning. Finally, we would like to thank Les Trois Brasseurs for stimulating our creativity.

• Bastien et al. [2012] Bastien, F., Lamblin, P., Pascanu, R., Bergstra, J., Goodfellow, I. J., Bergeron, A., Bouchard, N., and Bengio, Y. (2012). Theano: new features and speed improvements. Deep Learning and Unsupervised Feature Learning NIPS 2012 Workshop.
• Bengio [2009] Bengio, Y. (2009). Learning deep architectures for AI. Now Publishers.
• Bengio et al. [2013a] Bengio, Y., Mesnil, G., Dauphin, Y., and Rifai, S. (2013a). Better mixing via deep representations. In ICML’13.
• Bengio et al. [2013b] Bengio, Y., Yao, L., Alain, G., and Vincent, P. (2013b). Generalized denoising auto-encoders as generative models. In NIPS26. Nips Foundation.
• Bengio et al. [2014a] Bengio, Y., Thibodeau-Laufer, E., and Yosinski, J. (2014a). Deep generative stochastic networks trainable by backprop. In ICML’14.
• Bengio et al. [2014b] Bengio, Y., Thibodeau-Laufer, E., Alain, G., and Yosinski, J. (2014b). Deep generative stochastic networks trainable by backprop. In Proceedings of the 30th International Conference on Machine Learning (ICML’14).
• Bergstra et al. [2010] Bergstra, J., Breuleux, O., Bastien, F., Lamblin, P., Pascanu, R., Desjardins, G., Turian, J., Warde-Farley, D., and Bengio, Y. (2010). Theano: a CPU and GPU math expression compiler. In Proceedings of the Python for Scientific Computing Conference (SciPy). Oral Presentation.
• Breuleux et al. [2011] Breuleux, O., Bengio, Y., and Vincent, P. (2011). Quickly generating representative samples from an RBM-derived process. Neural Computation, 23(8), 2053–2073.
• Glorot et al. [2011] Glorot, X., Bordes, A., and Bengio, Y. (2011). Deep sparse rectifier neural networks. In AISTATS’2011.
• Goodfellow et al. [2013a] Goodfellow, I. J., Warde-Farley, D., Mirza, M., Courville, A., and Bengio, Y. (2013a). Maxout networks. In ICML’2013.
• Goodfellow et al. [2013b] Goodfellow, I. J., Mirza, M., Courville, A., and Bengio, Y. (2013b). Multi-prediction deep Boltzmann machines. In NIPS’2013.
• Goodfellow et al. [2013c] Goodfellow, I. J., Warde-Farley, D., Lamblin, P., Dumoulin, V., Mirza, M., Pascanu, R., Bergstra, J., Bastien, F., and Bengio, Y. (2013c). Pylearn2: a machine learning research library. arXiv preprint arXiv:1308.4214.
• Gutmann and Hyvarinen [2010] Gutmann, M. and Hyvarinen, A. (2010). Noise-contrastive estimation: A new estimation principle for unnormalized statistical models. In AISTATS’2010.
• Hinton et al. [2012a] Hinton, G., Deng, L., Dahl, G. E., Mohamed, A., Jaitly, N., Senior, A., Vanhoucke, V., Nguyen, P., Sainath, T., and Kingsbury, B. (2012a). Deep neural networks for acoustic modeling in speech recognition. IEEE Signal Processing Magazine, 29(6), 82–97.
• Hinton et al. [1995] Hinton, G. E., Dayan, P., Frey, B. J., and Neal, R. M. (1995). The wake-sleep algorithm for unsupervised neural networks. Science, 268, 1558–1161.
• Hinton et al. [2006] Hinton, G. E., Osindero, S., and Teh, Y. (2006). A fast learning algorithm for deep belief nets. Neural Computation, 18, 1527–1554.
• Hinton et al. [2012b] Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2012b). Improving neural networks by preventing co-adaptation of feature detectors. Technical report, arXiv:1207.0580.
• Hyvärinen [2005] Hyvärinen, A. (2005). Estimation of non-normalized statistical models using score matching. J. Machine Learning Res., 6.
• Jarrett et al. [2009] Jarrett, K., Kavukcuoglu, K., Ranzato, M., and LeCun, Y. (2009). What is the best multi-stage architecture for object recognition? In Proc. International Conference on Computer Vision (ICCV’09), pages 2146–2153. IEEE.
• Kingma and Welling [2014] Kingma, D. P. and Welling, M. (2014). Auto-encoding variational bayes. In Proceedings of the International Conference on Learning Representations (ICLR).
• Krizhevsky and Hinton [2009] Krizhevsky, A. and Hinton, G. (2009). Learning multiple layers of features from tiny images. Technical report, University of Toronto.
• Krizhevsky et al. [2012] Krizhevsky, A., Sutskever, I., and Hinton, G. (2012). ImageNet classification with deep convolutional neural networks. In NIPS’2012.
• LeCun et al. [1998] LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278–2324.
• Rezende et al. [2014] Rezende, D. J., Mohamed, S., and Wierstra, D. (2014). Stochastic backpropagation and approximate inference in deep generative models. Technical report, arXiv:1401.4082.
• Rifai et al. [2012] Rifai, S., Bengio, Y., Dauphin, Y., and Vincent, P. (2012). A generative process for sampling contractive auto-encoders. In ICML’12.
• Salakhutdinov and Hinton [2009] Salakhutdinov, R. and Hinton, G. E. (2009). Deep Boltzmann machines. In AISTATS’2009, pages 448–455.
• Smolensky [1986] Smolensky, P. (1986). Information processing in dynamical systems: Foundations of harmony theory. In D. E. Rumelhart and J. L. McClelland, editors, Parallel Distributed Processing, volume 1, chapter 6, pages 194–281. MIT Press, Cambridge.
• Susskind et al. [2010] Susskind, J., Anderson, A., and Hinton, G. E. (2010). The Toronto face dataset. Technical Report UTML TR 2010-001, U. Toronto.
• Tieleman [2008] Tieleman, T. (2008). Training restricted Boltzmann machines using approximations to the likelihood gradient. In W. W. Cohen, A. McCallum, and S. T. Roweis, editors, ICML 2008, pages 1064–1071. ACM.
• Vincent et al. [2008] Vincent, P., Larochelle, H., Bengio, Y., and Manzagol, P.-A. (2008). Extracting and composing robust features with denoising autoencoders. In ICML 2008.
• Younes [1999] Younes, L. (1999). On the convergence of Markovian stochastic algorithms with rapidly decreasing ergodicity rates. Stochastics and Stochastic Reports, 65(3), 177–228.

Copyright Privacy Policy

Generated on Fri Mar 8 00:21:12 2024 by LaTeXML